这篇博客整理一下在拓扑材料Bi$_2$Se$_3$计算中,通过能带成分和对称性分析,再结合微扰论来推导低能有效模型,主要是对文章进行翻译,过程中会加一点自己的笔记.

虽然对拓扑绝缘体的材料和对应的模型都很熟了,但是始终没有掌握如何从具体的材料出发,来得到其对应的低能哈密顿量,从而可以在材料的基础上,对模型进行研究.这里就想通过精读Model Hamiltonian for topological insulators这篇文章,来掌握一下这个方法.

晶体结构

首先来明确材料Bi$2$Se$_3$的晶体结构等信息.首先在Material Project这个网站中找到这个材料,其晶体结构时菱形的,对应的空间群是$D{3d}^5(R\bar{3}m)$,其晶体结构如下图所示,沿着$z$方向是个层状结构,每个元胞中有5个原子,

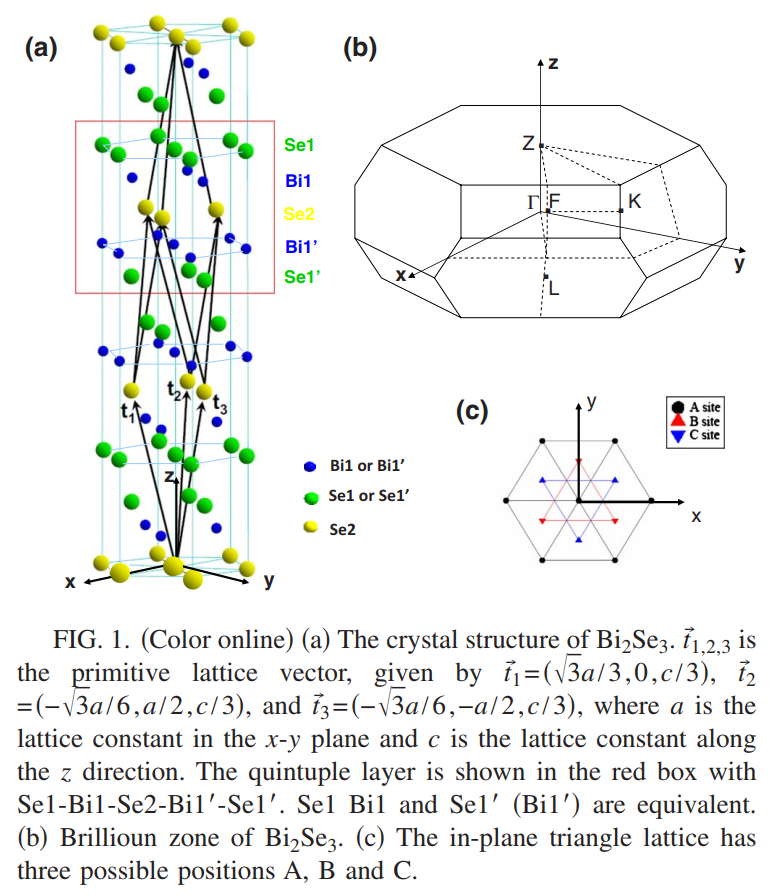
两个蓝色标记的等价Bi原子(Bi1,Bi$1^\prime $),两个绿色标记的等价Se原子(Se1,Se$1^\prime $),还有一个黄色的Se原子,它与Se1原子是不等价的,5个原子层构成一个元胞,通常被称为quintuple layer.

沿着$z$方向看,每个原子层都形成了三角晶格,而且每一层的排列方式都是不同的.

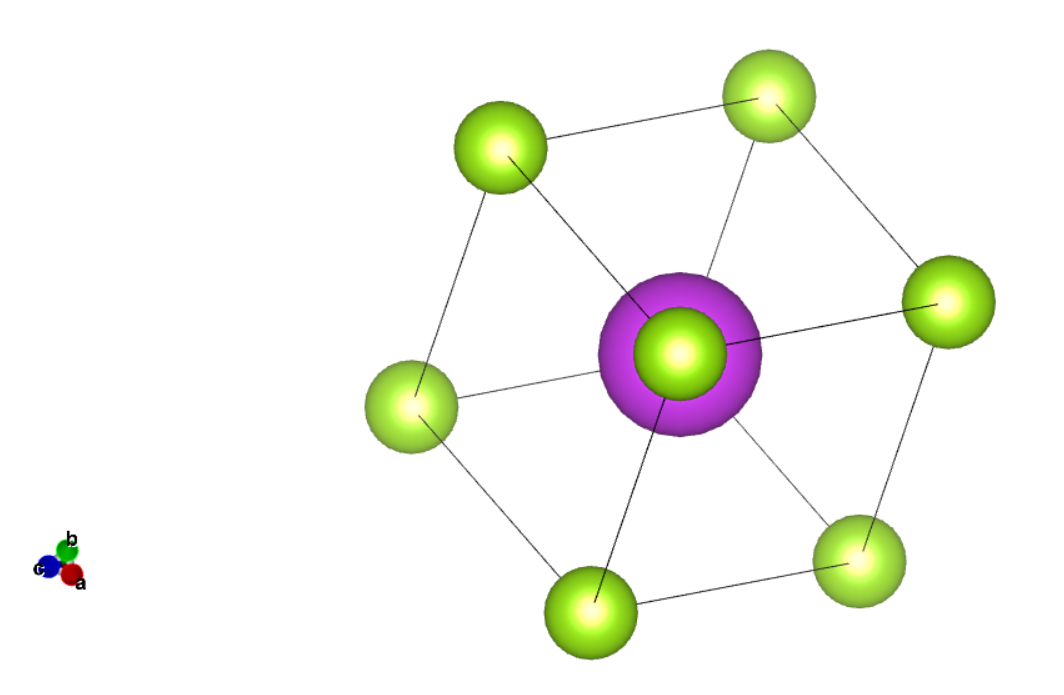
沿着$z$方向,这些三角层以$A-B-C-A-B-C-\cdots$的方式进行堆叠,此时元胞基矢$t_i,i=1,2,3$并不是沿着$z$方向的.比如在五元层中Se2原子占据了$A$位置,那么在下一个五元层他就会占据$c$或者$B$,而不会继续占据$A$位置.这里直角坐标轴的选取如下:$z$方向是垂直于原子层的,$x$轴是沿着一个二元轴,具有两重旋转对称,$y$轴是沿着等分线轴,它是反射面与Se2原子层的交线.

对称性

这个晶体结构具有下面的一些离散对称性:

• 沿$z$方向三重旋转$R_3^z$ $R_3^z$可以通过下面的变换产生:$x\rightarrow x\cos\theta-y\sin\theta,y\rightarrow x\sin\theta+y\cos\theta,z\rightarrow z,\theta=\frac{2\pi}{3}$
• 沿着$x$方向的两重旋转$R_2^x$ 这个操作对应着$x$方向不动,$z,y$方向都反演,$x\rightarrow x,z\rightarrow -z,y\rightarrow -y$,此时原子层的变换为$Se2\rightarrow Se2,Bi1\rightarrow Bi1^\prime ,Se1\rightarrow Se1^\prime $,在这个操作下发现原子层Bi1(Se1)和Bi1’(Se1’)相互交换了位置.
• 反演对称$P$ 以Se2位置作为反演中心,$Se2\rightarrow Se2,Bi1\rightarrow Bi1^\prime ,Se1\rightarrow Se^\prime $,在反演操作下Bi1(Se1)变换到$Bi1^\prime (Se1^\prime )$.
• 时间反演对称$\mathcal{T}$ 时间反演操作为$\mathcal{T}=\Theta\mathcal{K},\Theta=i\sigma_2,\mathcal{K}$是复数共轭,这里$\sigma_i$矩阵代表的是自旋.

  原子轨道

  为了从物理图像上理解$Bi_2Se_3$的能带结构,首先来研究每个元素的轨道信息.Bi原子的电子结构维$6s^26p^3$,Se的为$4s^24p^4$,可以发现两种元素最外层电子都是$p$轨道的,因此在考虑能带的时候,就可以只关心$p$轨道电子的贡献,而忽略其余轨道.因为$Bi_2Se_3$是个层状结构,在单个的五元层中,化学键是比较强的,但是在相邻两个五元层之间仅通过较弱的范德瓦尔斯力耦合在一起,因此可以只关心单个五元层的信息.在一个五元层中又一个元胞中存在5个原子,前面也提到过只需要关注$p$轨道即可($p_x,p_y,p_z$),因此这里一个元胞中会有15个轨道,首先忽略电子自旋,在之后考虑自旋轨道耦合(SOC)时再进行自旋的研究.这里标记一下轨道$\rvert\Lambda,\alpha\rangle,\Lambda=Bi1,Bi1^\prime ,Se1,Se1^\prime ,Se2,\alpha=p_x,p_y,p_z$.通过晶体结构可以发现,$Se2$在五元层的中间,被夹在两层Bi($Bi1,Bi1^\prime$)之间,而两个$Se(Se1,Se1^\prime )$位于最外层.由于所有的Se原子层都被Bi原子层分开了,所以体系中耦合最强的就是Bi原子层与Se原子层.这样的耦合会产生能级排斥效应,使得$Bi$的能级被推高形成新的态$\rvert B_\alpha\rangle,\rvert B^\prime \rangle$,而$Se$的能级则被压低形成三个态$\rvert S_\alpha\rangle,\rvert S_\alpha^\prime \rangle,\rvert S0_\alpha\rangle$,如下图所示.

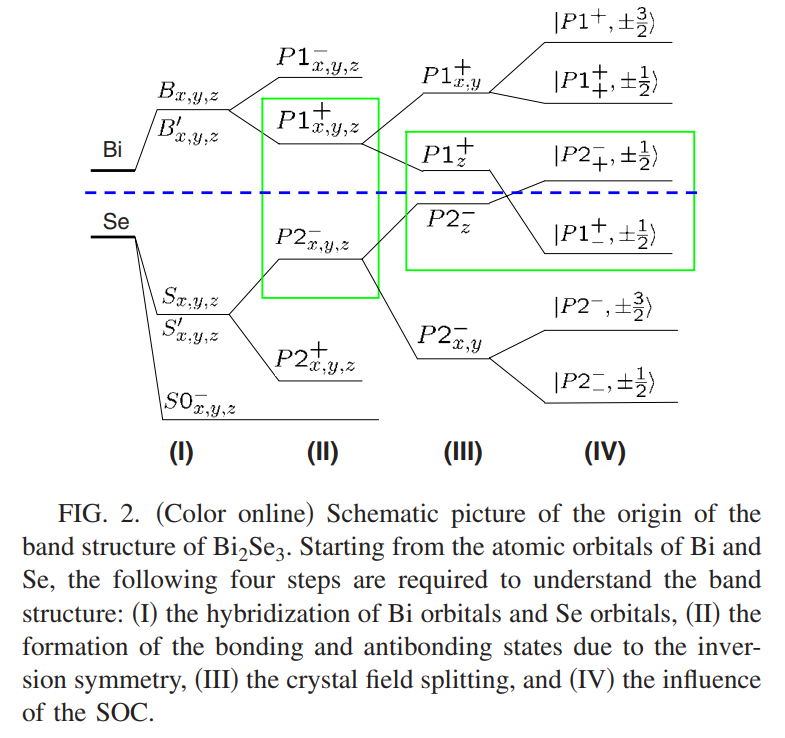
因为系统具有反演对称,可以方便的讲这些轨道组合,形成具有确定宇称的成键态与反键态

\[\rvert P1^\pm,\alpha\rangle=\frac{1}{\sqrt{2}}(\rvert B_\alpha\rangle\mp\rvert B^\prime _\alpha\rangle),\quad \rvert P2^\pm,\alpha\rangle=\frac{1}{\sqrt{2}}(\rvert S_\alpha\rangle\mp\rvert S^\prime _\alpha\rangle)\]

这里上标的正负号对应着态的宇称,$\alpha=p_x,p_y,p_z$.当$\rvert B_\alpha(S_\alpha)\rangle$与$\rvert B^\prime \alpha(S^\prime _\alpha)\rangle$之间的耦合被考虑之后,成键态与反键态对应的能量劈裂来,反键态比成键态具有更高的能量,如上图II阶段所示.此时$\rvert P1^+,\alpha\rangle,\rvert P2^-,\alpha\rangle,(\alpha=p_x,p_y,p_z)$是靠近费米面的,所以可以只关注这些态,而忽略那些远离费米面附近的能带的贡献.因为晶体是个层状结构,在原子平面上$z$方向与$x,y$方向是不同的,因此对$P1^+,P2^-$态,$p_z$轨道的能量分离与$p_x,p_y$轨道是不同的.这里$\rvert P1^+,p{x,y}\rangle$轨道的能量比$\rvert P1^+,p_z\rangle$的能量高,而$\rvert P2^-,p_{x,y}\rangle$比$\rvert P2^-,p_z\rangle$的能量低,因此导带只考虑$\rvert P1^+,p_z\rangle$,价带只考虑$\rvert P2^-,p_z\rangle$,如上图III所示.

在上面的原子轨道的基础上开始考虑SOC效应,给每个态再赋予自旋指标,态$\rvert P1^+,\alpha,\sigma\rangle,\rvert P2^-,\alpha,\sigma\rangle$都是双重简并的,$\sigma=\uparrow,\downarrow$表示的是自旋. 原子的SOC哈密顿量为$\hat{H}{SOC}=\lambda{\bf s\cdot L},\lambda=\frac{1}{2m_0^2c^2r}\frac{\partial U}{\partial r}$依赖于原子的势场$U$,它会将原子的轨道和自旋耦合起来.将轨道$p_x,p_y$转换成$p{\pm}$来定义轨道角动量

\[\rvert \Lambda,p_+,\sigma\rangle=-\frac{1}{\sqrt{2}}(\rvert\Lambda,p_x,\sigma\rangle+i\rvert\Lambda,p_y,\sigma\rangle),\quad\rvert \Lambda,p_{-},\sigma\rangle=\frac{1}{\sqrt{2}}(\rvert\Lambda,p_x,\sigma\rangle-i\rvert\Lambda,p_y,\sigma\rangle),\quad\Lambda=P1^+,P2^-\]

在这个基矢下,原子SOC的哈密顿量为

\[\langle\Lambda,p_+,\uparrow\rvert H_{SOC}\rvert\Lambda,p_+,\uparrow\rangle=\langle\Lambda,p_{-},\downarrow\rvert H_{SOC}\rvert\Lambda,p_{-},\downarrow\rangle\equiv\frac{\lambda_\Lambda}{2}\\ \langle\Lambda,p_+,\downarrow\rvert H_{SOC}\rvert\Lambda,p_+,\downarrow\rangle=\langle\Lambda,p_{-},\uparrow\rvert H_{SOC}\rvert\Lambda,p_{-},\uparrow\rangle\equiv-\frac{\lambda_\Lambda}{2}\\ \langle\Lambda,p_+,\downarrow\rvert H_{SOC}\rvert\Lambda,p_z,\uparrow\rangle=\langle\Lambda,p_{-},\uparrow\rvert H_{SOC}\rvert\Lambda,p_{z},\downarrow\rangle\equiv\frac{\lambda_\Lambda}{2}\\ \langle\Lambda,p_z\uparrow(\downarrow)\rvert\rvert H_{SOC}\rvert\Lambda,p_z,\uparrow(\downarrow)\rangle=0\]

对BI和Se原子,$\lambda_\Lambda$的值是其SOC系数的线性组合,它决定于在Se和Bi中有多少轨道混合到了态$\rvert \Lambda\rangle$,而$\lambda_\Lambda$的符号对$\Lambda=P1^+,P2^{-}$始终是正的,因为原子间的势能是吸引相互作用.这里可以发现沿着$z$方向的总角动量是守恒的,因为耦合只发生在$\rvert\Lambda,p_z,\uparrow\rangle(\rvert\Lambda,p_z,\downarrow\rangle)$和$\rvert\Lambda,p_{+},\downarrow\rangle(\rvert\Lambda,p_{-},\uparrow\rangle)$之间.当考虑了SOC之后,新的本征态为

\[\rvert\Lambda,\frac{3}{2}\rangle=\rvert\Lambda,p_{+},\uparrow\rangle,\quad\rvert\Lambda,-\frac{3}{2}\rangle=\rvert\Lambda,p_{-},\downarrow\rangle,\quad\rvert\Lambda_{+},\frac{1}{2}\rangle=u^\Lambda_{+}\rvert\Lambda,p_z,\uparrow\rangle+v^\Lambda_{+}\rvert\Lambda,p_{+},\downarrow\rangle\\ \rvert\Lambda_{-},\frac{1}{2}\rangle=u^\Lambda_{-}\rvert\Lambda,p_z,\uparrow\rangle+v^\Lambda_{-}\rvert\Lambda,p_{+},\downarrow\rangle,\quad \rvert\Lambda_{+},-\frac{1}{2}\rangle=(u^\Lambda_{+})^*\rvert\Lambda,p_z,\downarrow\rangle+(v^\Lambda_{+})^*\rvert\Lambda,p_{+},\uparrow\rangle\\ \rvert\Lambda_{-},-\frac{1}{2}\rangle=(u^\Lambda_{-})^*\rvert\Lambda,p_z,\downarrow\rangle+(v^\Lambda_{-})^*\rvert\Lambda,p_{-},\uparrow\rangle\label{a1}\]

对应的本征值为$E^\Lambda_{3/2},E^{\Lambda_\pm}_{1/2}$,每个能级都是双重简并的,系数$u,v$可以通过求解下面$2\times 2$哈密顿量得到

\[\hat{H}=\left(\begin{array}{cc}E_{\Lambda,x}-\lambda_\Lambda/2&\lambda_\Lambda/\sqrt{2}\\ \lambda_\Lambda/\sqrt{2}& E_{\Lambda,z}\end{array}\right)\]

对前面的本征态,所有关于SOC的信息都包含在$u,v$中,它们的值为

\[\left(\begin{array}{c}u_\pm^\Lambda\\ v_\pm^\Lambda\end{array}\right)=\frac{1}{N_\pm}\left(\begin{array}{c}\Delta E_\Lambda\pm\sqrt{(\Delta E)^2+\frac{\lambda_\Lambda^2}{2}}\\ \lambda_\Lambda/\sqrt{2}\end{array}\right)\]

$N_\pm=\lambda_\Lambda^2+2\Delta E^2\lambda\pm 2\Delta E\Lambda\sqrt{\Delta E^2\Lambda+\lambda\Lambda^2/2}, \Delta E_\Lambda=\frac{E_{\Lambda,x}-E_{\Lambda,z}-\lambda_\Lambda/2}{2}$,这里轨道$p_{x(y)}$与$p_z$的能级分裂是因为晶体 场效应比SOC是要大的,劈裂能量$\Delta E_\Lambda$主要是有$E_{\Lambda,x}-E_{\Lambda,z}$决定.到这里可以发现$\rvert\Lambda,p_z, \uparrow\rangle(\rvert\Lambda,p_z,\downarrow\rangle)$与$\rvert\Lambda,p_{+},\downarrow\rangle(\rvert\Lambda,p_{-}, \uparrow\rangle)$之间的SOC效应会进一步诱导这两个态之间的能级排斥,最终$\rvert P1^+{-},\pm\frac{1}{2}\rangle$将会压低, $\rvert P2^{-}+,\pm\frac{1}{2}\rangle$将会被推高,当SOC效应足够强的时候,就会发生这一对态之间的能级交叉,如上图IV所示.

因为这两个态具有相反的宇称(上标索引表示宇称),两者之间会发生能带反转没类似于HgTe量子阱.这也是$Bi_2Se_3$材料家族称为拓扑绝缘体相的重要特征.在接下来的分析中就会只关注这个四个态,而将其余的态作为微扰处理.

基于对称性的哈密顿量推导

根据前面的讨论以及第一性原理计算的能带结果,将费米面附近的能带标记为$\rvert\Lambda^\pm,\alpha\rangle,\Lambda=P1\pm,P2\pm,\alpha=\pm\frac{1}{2},\pm\frac{3}{2}$,如下图所示

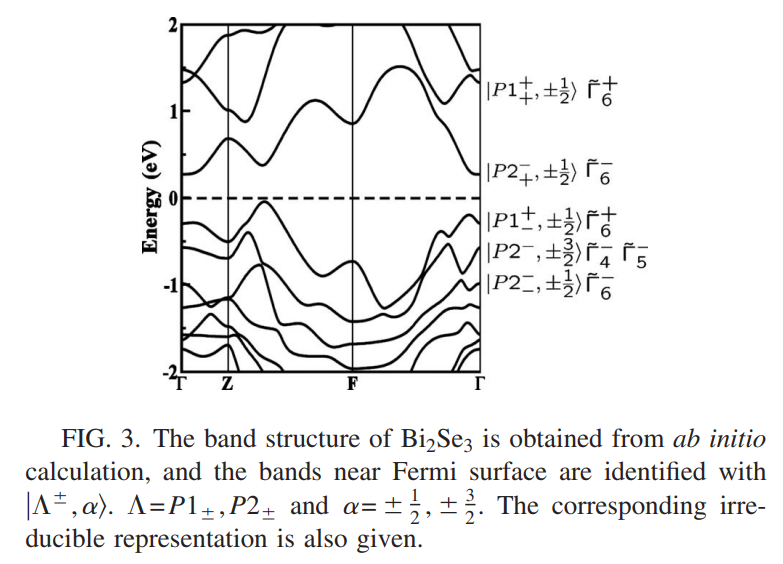
总之,这些态是有Bi和Se原子的$p$轨道组成的成键轨道和反键轨道,然而它们的$s$也会混合进来,为了明确每个条能,将其与晶体对称性的表示联系起来.在$\Gamma$点个态都应该属于晶体对称群的一个不可约表示,这些轨道将的混合仍然会保持对称性.则利用警惕的对称性是区分能带的一个合适的方法.首先根据晶体空间群$D_{3d}^5$的不可约表示来确定没一条能带,之后从对称性原理出发来推导哈密顿量的形式.

首先来考虑无自旋的时候,态为$\rvert\Lambda^\pm,\alpha\rangle,\Lambda=P1,P2,\alpha=p_x,p_y,p_z$.晶体$Bi_2Se_3$的空间群为$D_{3d}^5$,对应的特征表如下

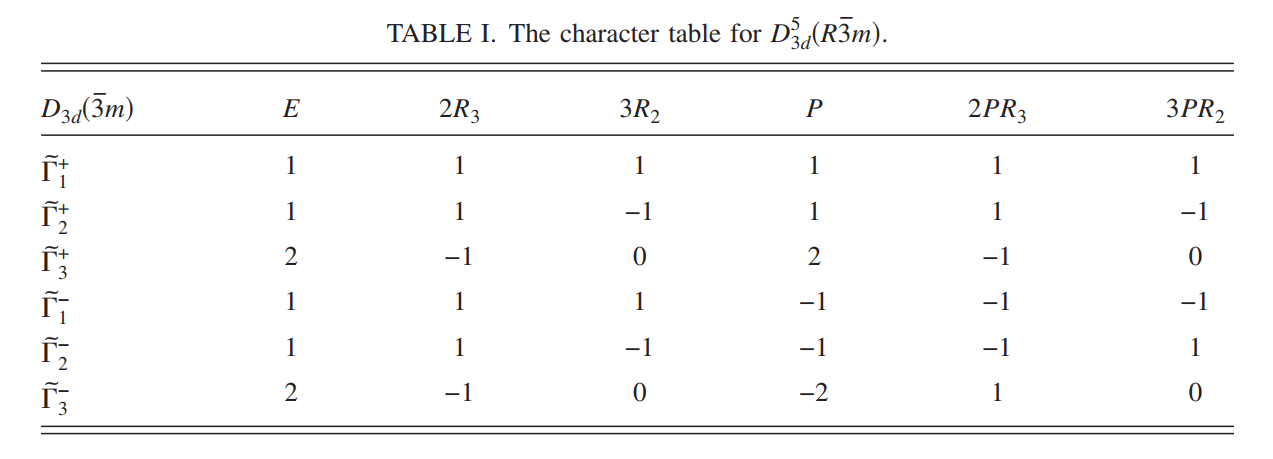
因为晶体是存在反演对称的,所以每个表示都具有确定的宇称本征值.对每个宇称,存在两个一维表示$\tilde{\Gamma}_1^\pm,\tilde{\Gamma}_2^\pm$,一个两维表示$\tilde{\Gamma}_3^\pm$,这里标记的上标则表示着宇称(+是偶,-是奇).根据前面每个原子轨道波函数的构建,可以通过点群生成元$R_3,R_2,P$来决定波函数在生成元变换下的性质.

群生成元:群宠所有的元素,可以通过生成元之间的组合得到.

空间群的不可约表示可以通过其对应点群的不可约表示诱导得到.

首先来看操作$R_2$对态$\rvert P1^\pm,p_x\rangle=\frac{1}{\sqrt{2}}(\rvert B_x\rangle-\rvert B^\prime \rangle)$的作用.$R_2$旋转不会改变$p_x$轨道,它只会交换$Bi1(Se1)$和$Bi1^\prime (Se1^\prime )$的位置,将$\rvert B\rangle$变换成$\rvert B^\prime \rangle$,因此有$R_2\rvert P1^+,p_x\rangle=-\rvert P1^+,p_x\rangle$.同样的讨论可以应用到其他的态上,下面列举这些态在晶体对称操作下的性质:

• 三种旋转$R_3$:$\rvert\Lambda^\pm,p_x\rangle\rightarrow\cos\theta\rvert \Lambda^\pm,p_x\rangle-\sin\theta\rvert\Lambda^\pm,p_y\rangle,\rvert\Lambda^\pm,p_y\rangle\rightarrow\sin\theta\rvert\Lambda^\pm,p_x\rangle+\cos\theta\rvert\Lambda^\pm,p_y\rangle,\rvert\Lambda^\pm,p_z\rangle\rightarrow\rvert\Lambda^\pm,p_z\rangle,\theta=2\pi/3$

• 两重旋转$R_2$:$\rvert\Lambda^\pm,p_x\rangle\rightarrow\mp\rvert\Lambda^\pm,p_x\rangle,\rvert\Lambda^\pm,p_y\rangle\rightarrow\pm\rvert\Lambda^\pm,p_y\rangle,\rvert\Lambda^\pm,p_z\rangle\rightarrow\pm\rvert\Lambda^\pm,p_z\rangle$

• 反演对称$P$:$\rvert\Lambda^\pm,\alpha\rangle\rightarrow\pm\rvert\Lambda^\pm,\alpha\rangle,\alpha=p_x,p_y,p_z$

这里$\Lambda=P1{\pm},P2{\pm}$;通过上面的分析,可以发现$\rvert\Lambda^{+(-)},p_x\rangle,\rvert\Lambda^{+(-)}, p_y\rangle$属于$\tilde{\Gamma}^{+(-)}_3$不可约表示,$\rvert\Lambda^+,p_z\rangle$属于$\tilde{\Gamma}^+_1$不可约表示, $\rvert\lambda^{-},p_z\rangle$属于$\tilde{\Gamma}_2^{-}$不可约表示.

当考虑了自旋之后,需要引入自旋表示$\tilde{\Gamma}^+6$,在旋转$\mathcal{C}=2\pi$时,它将会改变符号. 空间群$D{3d}^5$的双群可以通过$\tilde{\Gamma}^{+}6$与$\tilde{\Gamma}^{\pm}{1,2,3}$的直积得到

\[\tilde{\Gamma}^\pm_3\otimes\tilde{\Gamma}^{+}_6=\tilde{\Gamma}^\pm_4+\tilde{\Gamma}^\pm_5+\tilde{\Gamma}^\pm_6\\ \tilde{\Gamma}^\pm_1\otimes \tilde{\Gamma}^+_6=\tilde{\Gamma}^\pm_6\\ \tilde{\Gamma}^\pm_2\otimes \tilde{\Gamma}^+_6=\tilde{\Gamma}^\pm_6\label{a2}\]

可以发现$\tilde{\Gamma}^\pm_3\otimes\tilde{\Gamma}^+6$会产生两个新的一维不可约表示$\tilde{\Gamma}^\pm_4,\tilde{\Gamma}^\pm_5$,它们是相互共轭的.$D{3d}^5$的双群特征表如下

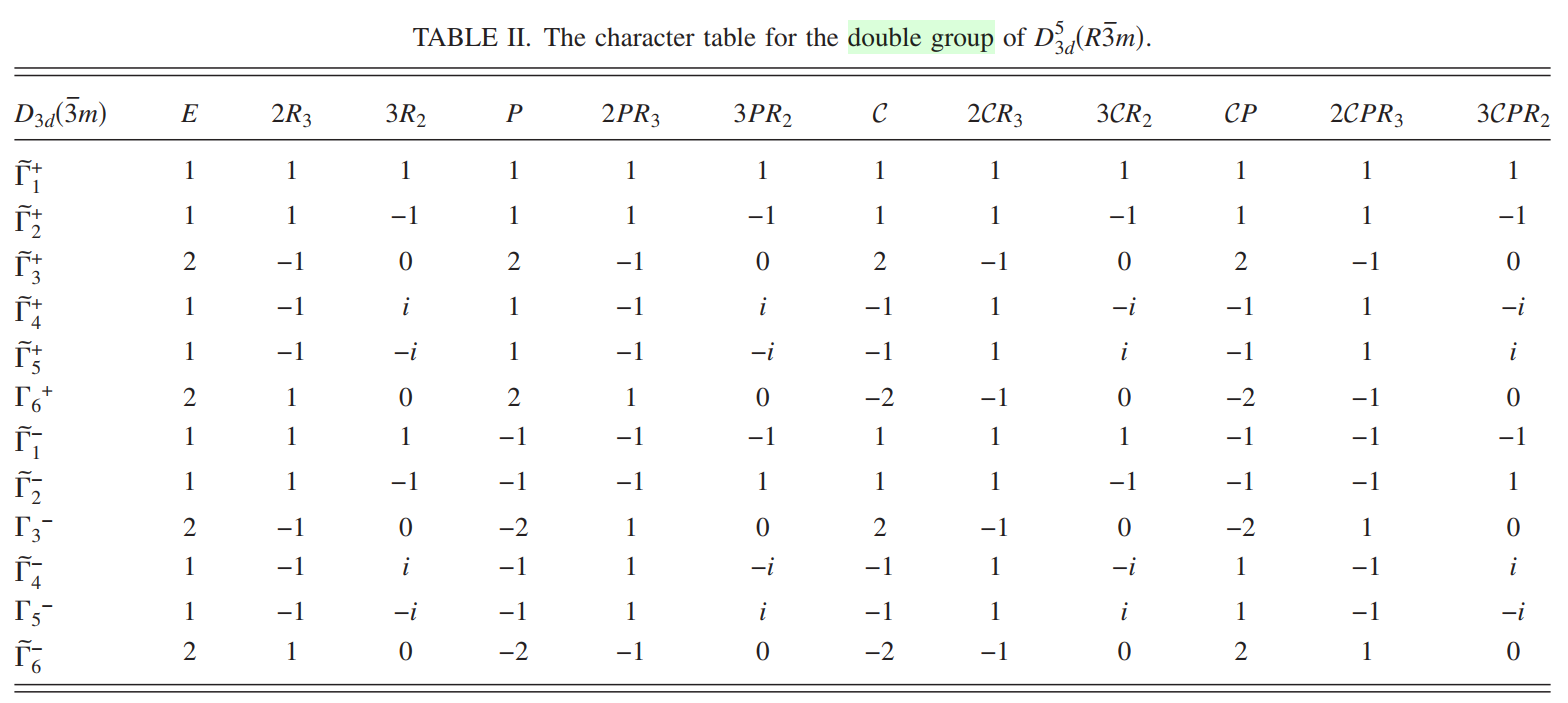
在考虑了SOC之后,本征态(\ref{a1})可以被分解到这个直积表示上,从双群构建直积表示的过程中可以发现,$\tilde{\Gamma}^\pm_{1,2} \otimes\tilde{\Gamma}^\pm_6$总是给出$\tilde{\Gamma}^\pm_6$,因此$\rvert\Lambda^+,\pm\frac{1}{2}\rangle,\Lambda=P1,P2$应 该属于$\tilde{\Gamma}^+6$表示,而$\rvert\Lambda^{-},\pm\frac{1}{2}\rangle,\Lambda=P1,P2$应该属于$\tilde{\Gamma}^{-}_6$ 表示.态$\rvert\Lambda^\pm,\pm 3/2\rangle$来源于$\rvert\Lambda,p{x,y}\rangle$与自旋的组合,根据(\ref{a2})可以得到$\rvert\Lambda^\pm,\pm3/2\rangle$应该是$\tilde{\Gamma}_4^\pm,\tilde{\Gamma}_5^\pm$表示的组合.通过在$R_2,R_3$的 变换分析,可以得到

\[\rvert\Lambda^\pm,\tilde{\Gamma}_4\rangle=\frac{1}{\sqrt{2}}(\rvert\Lambda^\pm,3/2\rangle+\rvert\Lambda^\pm,-3/2\rangle)\]

属于$\tilde{\Gamma}^\pm_4$表示,

\[\rvert\Lambda^\pm,\tilde{\Gamma}_5\rangle=\frac{1}{\sqrt{2}}(\rvert\Lambda^\pm,3/2\rangle-\rvert\Lambda^\pm,-3/2\rangle)\]

属于$\tilde{\Gamma}_5$表示.上面的结果可以同归对(\ref{a1})的变换来研究其变换

• 三重旋转$R_3$:

\[\rvert\Lambda,\pm\frac{1}{2}\rangle\rightarrow e^{\pm i\pi/3}\rvert\Lambda,\pm\frac{1}{2},\rvert\Lambda,\pm\frac{3}{2}\rightarrow-\rvert\Lambda,\pm\frac{3}{2},\Lambda=P1^\pm_\pm\]

• 两重旋转$R_2$:

\[\rvert\Lambda^+,\pm\frac{1}{2}\rangle\rightarrow i\rvert\Lambda^+,\mp\frac{1}{2}\rangle,\rvert\Lambda^{-},\pm\frac{3}{2}\rangle\rightarrow-i\rvert\Lambda^{-},\mp\frac{1}{2}\rangle,\rvert\Lambda^+,\pm\frac{3}{2}\rangle\rightarrow i\rvert\Lambda^+,\mp\frac{3}{2}\rangle,\rvert\Lambda^{-},\pm\frac{3}{2}\rangle\rightarrow -i\rvert\Lambda^{-},\mp\frac{3}{2}\rangle,\Lambda=P1_\pm,P2_\pm\]

• 反演对称$P$:

\[\rvert\Lambda^\pm,\alpha\rangle\rightarrow\pm\rvert\Lambda^\pm,\alpha\rangle,\Lambda=P1_\pm,P2_\pm,\alpha=\pm\frac{1}{2},\pm\frac{3}{2}\]

在通常的金刚石或者闪锌矿结构中轨道$p$与自旋的耦合通常给出四维表示$\tilde{\Gamma}_8$和两维表示$\tilde{\Gamma}_7$,在现在的情况中,因为晶体具有更低的对称性,$\tilde{\Gamma}_7$表示与$\tilde{\Gamma}_6$相表示相同,$\tilde{\Gamma}_8$表示约化为两个一维表示$\tilde{\Gamma}_4$和$\tilde{\Gamma}_5$以及一个两维表示$\tilde{\Gamma}_6$.在下图中给出了费米面附近能带对应的不可约表示以及基函数

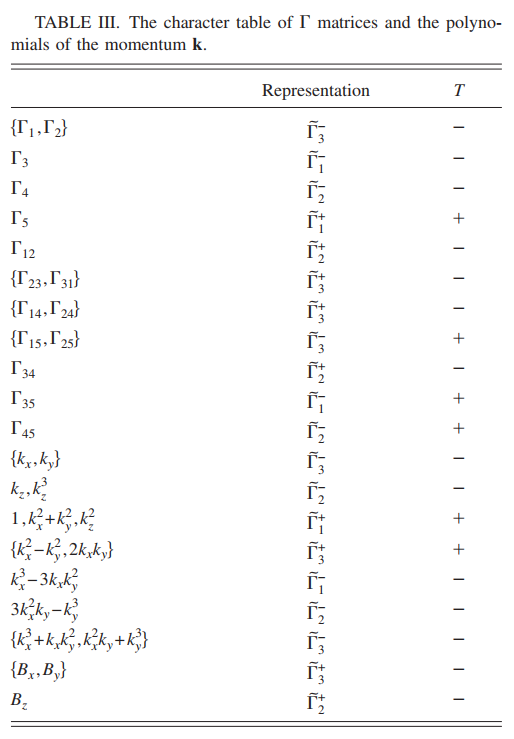
接下来开始通过在$\Gamma$点波函数的对称性来分析$Bi_2Se_3$的低能物理,并构建哈密顿量.根据前面的讨论,在费米面附近,导带和价带主要由 $\rvert P1{-}^+,\pm\frac{1}{2}\rangle,\rvert P2{+}^{-},\pm\frac{1}{2}\rangle$决定,它们分别属于$\tilde{\Gamma}_6^+, \tilde{\Gamma}_6^{-}$不可约表示,因此$Bi_2Se_3$对应的最小哈密顿量就是以这四个态为基矢.通常$4\times 4$哈密顿量可以利用 $\Gamma$矩阵进行展开

\[H_\text{eff}=\epsilon(\mathbf{k})\mathbb{I}+\sum_id_i(\mathbf{k})\Gamma_i+\sum_{ij}d_{ij}\Gamma_{ij}\]

$\Gamma_i,i=1,2,3,4,5$是Dirac矩阵,满足${\Gamma_i,\Gamma_j}=2\delta_{ij},\Gamma_{ij}=[\Gamma_i,\Gamma_j]/2i,\epsilon({\bf k}),d_i(\mathbf{k}),d_{ij}(\mathbf{k})$可以展开成动量$\mathbf{k}$的幂函数. 假设上面的哈密顿量是以

\[\rvert P1^+_{-},\frac{1}{2}\rangle,\rvert P2^{-}_+,\frac{1}{2}\rangle,\rvert P1^+_{-},-\frac{1}{2}\rangle,\rvert P2_+^{-},-\frac{1}{2}\rangle\]

为基矢,根据这些态在对称性操作下的变换,可以构建下面的变换矩阵

• 时间反演:$\mathcal{T}=\Theta\mathcal{K},\Theta=i\sigma_2\otimes\mathcal{I},\mathcal{K}$是复共轭算符.

• 三重旋转:$R_3=e^{i(\Pi/2)\theta},\Pi=\sigma_3\otimes\mathcal{I},\theta=2\pi/3.$

• 两重转动:$R_2=i\sigma_1\otimes\tau_3$.

• 反演操作:$P=\mathcal{I}\otimes\tau_3$.

在上面$\sigma$作用在自旋上,$\tau$作用在$P1^+,P2^{-}$上.根据上面的变换矩阵,可以得到每个$\Gamma$矩阵的不可约表示.根据哈密顿量在对称性操作下的不变性,$d_i(\mathbf{k})[d_{ij}(\mathbf{k})]$与其对应的$\Gamma_i[\Gamma_{ij}]$在对称操作下具有相同的行为,也就意味着它们属于相同的晶体点群不可约表示.在上图中列举出了$\Gamma$矩阵和$\mathbf{k}$的多项式的表示以及其在时间反演下的性质.因为研究的时候希望同时保留时间反演和晶体对称性,我们必须选择$\Gamma$矩阵和$\mathbf{k}$具有相同的表示.比如,$\Gamma_1,\Gamma_2$都属于$\tilde{\Gamma}_3^{-}$表示,且在时间反演下是奇的,$k_x,k_y$也相同.因此可以将它们组合,从而构成哈密顿量中的不变项.将哈密顿量构建到$k^3$,可以得到

\[H^\prime _\text{eff}=H_0^\prime +H_3^\prime \\ H_0^\prime =\epsilon_\mathbf{k}+M(\mathbf{k})\Gamma_5+B(k_z)\Gamma_4k_z+A(k_\parallel)(\Gamma_1k_y-\Gamma_2k_x)\\ H_3^\prime =R_1\Gamma_3(k_x^3-3k_xk_y^2)+R_2\Gamma_4(2k_x^2k_y-k_y^3)\]

这里$\epsilon_\mathbf{k}=C_0+C_1k_z^2=C_2k_\parallel^2,M(\mathbf{k})=M_0+M_1k_z^2+M_2k_\parallel^2,A(k_\parallel)=A_0+A_2k_\parallel^2,B(k_z)=N_0+B_2k_z^2,$,$k_\parallel^2=k_x^2+k_y^2$, 此时$H_0^\prime$仍然保持着沿$z$方向的面内旋转对称,然而$H_3^\prime $破坏了面内旋转对称,变成了三重旋转对称.

• 哈密顿量构建方法

在对每一项进行构建的时候,首先要确定多项式$\mathbf{k}$和其对应的矩阵要属于同一个不可约表示.一如$M(\mathbf{k})\Gamma_5$这一项, 从上面的表中可以发现$\Gamma_5$属于$\tilde{\Gamma^{+}1}$这个不可约表示,那么对应这个表示的多项式有$1,k_x^2+k_y^2,k_z^2$这三 项,那么就可以得到$M(\mathbf{k})$的一个表示$M(\mathbf{k})=M_0+M_1k_z^2+M_2k\parallel^2$.其余的项对应的构建方式也是完全相同.

${\bf k\cdot p}$微扰推导哈密顿量

${\bf k\cdot p}$的基本想法是利用在布里渊区中$\Gamma$点的波函数为零级波函数,将

\[\hat{H}^\prime =\frac{\hbar}{m_0}{\bf k\cdot p}\]

作为微扰,这里$\mathbf{p}=-i\hbar\partial_\mathbf{r}$是作用在零级波函数上的动量算符,晶体动量$\mathbf{k}$此时是个小参数作为微扰来处理.哈密顿量模型可以被展开成一系列$k$的幂函数.首先来考虑$D_{3d}^5$对称性对动量矩阵元的限制.先来标记本征态

\[\rvert\Lambda^\pm,\alpha\rangle,\Lambda=P1_\pm,P2_\pm,\alpha=\pm\frac{1}{2},\pm\frac{3}{2}\]

本征态$\rvert\Lambda,\pm 1/2\rangle$属于$\tilde{\Gamma}_6^\pm$表示,对于$\rvert\Lambda,\pm 3/2\rangle$态需要上面态的组合

\[\rvert\Lambda^\pm,\tilde{\Gamma}_4\rangle=\frac{1}{\sqrt{2}}(\rvert\Lambda^\pm,3/2\rangle+\rvert\Lambda^\pm,-3/2\rangle),\\ \Lambda^\pm,\tilde{\Gamma}_5\rangle=\frac{1}{\sqrt{2}}(\rvert\Lambda^\pm,3.2\rangle-\rvert\Lambda^\pm,-3/2\rangle)\]

分别属于$\tilde{\Gamma}_4,\tilde{\Gamma}_5$表示.

\[(\tilde{\Gamma}_6^\pm)^*\otimes\tilde{\Gamma}_6^\pm=\tilde{\Gamma}_1^{+}+\tilde{\Gamma}_2^{+}+\tilde{\Gamma}_3^{+}, (\tilde{\Gamma}_6^{+})^*\otimes \tilde{\Gamma}_1^{-}=\tilde{\Gamma}_1^{-}+\tilde{\Gamma}_2^{-}+\tilde{\Gamma}_3^{-}, (\tilde{\Gamma}_6^{+})^*\otimes \tilde{\Gamma}_4^{\pm}=\tilde{\Gamma}_3^{\pm}, (\tilde{\Gamma}_6^{-})^*\otimes \tilde{\Gamma}_4^{\pm}=\tilde{\Gamma}_3^{\pm},\\ (\tilde{\Gamma}_6^{+})^*\otimes \tilde{\Gamma}_5^{\pm}=\tilde{\Gamma}_3^{\pm}, (\tilde{\Gamma}_6^{-})^*\otimes \tilde{\Gamma}_5^{\pm}=\tilde{\Gamma}_3^{\pm}, (\tilde{\Gamma}_{4(5)}^{+})^*\otimes \tilde{\Gamma}_{4(5)}^{-}=\tilde{\Gamma}_1^{-}, (\tilde{\Gamma}_{4(5)}^{+})^*\otimes \tilde{\Gamma}_{5(4)}^{-}=\tilde{\Gamma}_2^{-}\]

上面给出了一些不可约表示的直积分解,也可以理解成态相乘,然后分解到对应的一些基本不可约表示上. 动量$p_x,p_y$属于$\tilde{\Gamma} 3^{-}$表示,$p_z$属于$\tilde{\Gamma}_2^{-}$表示,因此这里要求本征态的直积分解中同样包含$\tilde{\Gamma}_3^{-},\tilde {\Gamma}_2^{-}$得到非零的矩阵元(相容性原理).比如$\tilde{\Gamma}_6^{\pm}$和$\tilde{\Gamma}{4,5}^{\pm}$的直积并不包含 $\tilde{\Gamma}2^{-}$,因此矩阵元$\langle\Lambda_1,\pm 1/2\rvert p_z\rvert\Lambda_2,\tilde{\Gamma}{4,5}\rangle$总是等 于0.对称性操作可以进一步帮助得到矩阵元素和动量之间的关系.比如对于$R_3$旋转操作,可以得到

\[\begin{equation}\begin{aligned}\langle\Lambda_1^+,\frac{1}{2}\rvert p_x\rvert\Lambda_2,-\frac{1}{2}\rangle &=\langle\Lambda_1^+,\frac{1}{2}\rvert R_3^\dagger R_3p_xR_3^\dagger D_3\rvert\Lambda_2^{-},-\frac{1}{2}\rangle\\ &=e^{-i(2\pi/3)}\langle\Lambda_1^{+},\frac{1}{2}\rvert(p_x\cos\frac{2\pi}{3}-p_y\sin\frac{2\pi}{3})\rvert\Lambda_2^{-},-\frac{1}{2}\rangle\\ &\rightarrow\langle\Lambda_1^{+},\frac{1}{2}\rvert p_x\rvert\Lambda_2^{-},-\frac{1}{2}\rangle=i\langle\Lambda_1^+,\frac{1}{2}\rvert p_y\rvert\Lambda_2^{-},-\frac{1}{2}\rangle\end{aligned}\end{equation}\]

最后可以得到一些独立的矩阵元素

\[\langle\Lambda_1^+,\frac{1}{2}\rvert p_x\rvert\Lambda_2^{-},-\frac{1}{2}\rangle=\langle\Lambda_1^+,-\frac{1}{2}\rvert p_x\rvert\Lambda_2^{-},\frac{1}{2}\rangle\\ i\langle\Lambda_1^+,\frac{1}{2}\rvert p_y\rvert\Lambda_2^{-},-\frac{1}{2}\rangle=-i\langle\Lambda_1^+,-\frac{1}{2}\rvert p_y\rvert\Lambda_2^{-},\frac{1}{2}\rangle=P_{\Lambda_1^{+},\Lambda_2^{-}}\] \[\langle\Lambda_1^+,\frac{1}{2}\rvert p_z\rvert\Lambda^{-},\frac{1}{2}\rangle=-\langle\Lambda_1^+,-\frac{1}{2}\rvert p_z\rvert\Lambda^{-},-\frac{1}{2}\rangle=Q_{\Lambda_1^{+},\Lambda_2^{-}}\] \[\langle\Lambda_1^\pm,\frac{1}{2}\rvert p_x\rvert\Lambda_2^{\mp},\tilde{\Gamma}_4\rangle=-i\langle\Lambda_1^\pm,-\frac{1}{2}\rvert p_x\rvert\Lambda_2^{\mp},\tilde{\Gamma}_4\rangle\\ =-i\langle\Lambda_1^\pm,\frac{1}{2}\rvert p_y\rvert\Lambda_2^{\mp},\tilde{\Gamma}_4\rangle=\langle\Lambda_1^\pm,-\frac{1}{2}\rvert p_y\rvert\Lambda_2^{\mp},\tilde{\Gamma}_4\rangle=M_{\Lambda^\pm_1,\Lambda_2^\mp}\] \[\langle\Lambda_1^\pm,\frac{1}{2}\rvert p_x\rvert\Lambda_2^{\pm},\tilde{\Gamma}_5\rangle=i\langle\Lambda_1^\pm,-\frac{1}{2}\rvert p_x\rvert\Lambda_2^{\mp},\tilde{\Gamma}_5\rangle=-i\langle\Lambda_1^\pm,\frac{1}{2}\rvert p_y\rvert\Lambda_2^{\mp},\tilde{\Gamma}_5\rangle\\ =-\langle\Lambda_1^\pm,-\frac{1}{2}\rvert p_y\rvert\Lambda_2^{\mp},\tilde{\Gamma}_5\rangle=N_{\Lambda_1^\pm,\Lambda_2^\mp}\] \[\langle\Lambda_1^{+},\tilde{\Gamma}_4\rvert p_z\rvert\Lambda^{-},\tilde{\Gamma}_4\rangle=R_{\Lambda_1^{+},\Lambda_2^{-}}\] \[\langle\Lambda_1^+,\tilde{\Gamma}_5\rvert p_z\rvert\Lambda^{-},\tilde{\Gamma}_5\rangle=S_{\Lambda_1^+,\Lambda_2^{-}}\]

这里采用$p_\pm=p_x\pm p_y$

\[\langle\Lambda_1^{+},\frac{1}{2}\rvert p_+\rvert\Lambda_2^{-},-\frac{1}{2}\rangle=\langle\Lambda_1^{+},-\frac{1}{2}\rvert p_{-}\rvert\Lambda_2^{-},\frac{1}{2}\rangle=2P_{\Lambda_1^{+},\Lambda_2^{-}}\] \[\langle\Lambda_1^{+},\frac{1}{2}\rvert p_{-}\rvert\Lambda_2^{-},-\frac{1}{2}\rangle=\langle\Lambda_1^{+},-\frac{1}{2}\rvert p_{+}\rvert\Lambda_2^{-},\frac{1}{2}\rangle=0\] \[\langle\Lambda_1^{\pm},\frac{1}{2}\rvert p_{-}\rvert\Lambda_1^{+},\Gamma_4\rangle=-i\langle\Lambda_1^{\pm},-\frac{1}{2}\rvert p_{+}\rvert\Lambda_2^{\mp},\Gamma_4\rangle=2M_{\Lambda_1^{\pm},\Lambda_2^{\mp}}\] \[\langle\Lambda_1^{\pm},\frac{1}{2}\rvert p_{+}\rvert\Lambda_2^{+},\Gamma_4\rangle=-i\langle\Lambda_1^{\pm},-\frac{1}{2}\rvert p_{-}\rvert\Lambda_2^{\mp},\Gamma_4\rangle=0\] \[\langle\Lambda_1^{\pm},\frac{1}{2}\rvert p_{-}\rvert\Lambda_2^{+},\Gamma_5\rangle=i\langle\Lambda_1^{\pm},-\frac{1}{2}\rvert p_{+}\rvert\Lambda_2^{\mp},\Gamma_5\rangle=2N_{\Lambda_1^{\pm},\Lambda_2^{\mp}}\] \[\langle\Lambda_1^{\pm},\frac{1}{2}\rvert p_{+}\rvert\Lambda_2^{\mp},\Gamma_5\rangle=i\langle\Lambda_1^{\pm},-\frac{1}{2}\rvert p_{-}\rvert\Lambda_2^{\mp},\Gamma_5\rangle=0\]

时间反演表明

\[P_{\Lambda_1^+,\Lambda_2^{-}},Q_{\Lambda_1^+,\Lambda_2^{-}}\]

可以被选择为实数

\[P_{\Lambda_1^+,\Lambda_2^{-}}=P^{*}_{\Lambda_1^+,\Lambda_2^{-}},Q_{\Lambda_1^+,\Lambda_2^{-}}=Q^{*}_{\Lambda_1^+,\Lambda_2^{-}}\]

而

\[M_{\Lambda_1^\pm,\Lambda_2^\mp}=iN^{*}_{\Lambda_1^\pm,\Lambda_2^\mp},R_{\Lambda_1^+\Lambda_2^{-}}=-S^{*}_{\Lambda_1^+,\Lambda_2^{-}}$.由于$\rvert P1_{-}^+,\pm\frac{1}{2}\rangle,\rvert P2_{+}^{-},\pm\frac{1}{2}\rangle\]

之间的矩阵元是比较重要的,这里进行一下标记

\[\langle P1_{-}^{+},\frac{1}{2}\rvert p_x\rvert P2_{+}^{-},-\frac{1}{2}\rangle=\langle P1_{-}^{+},-\frac{1}{2}\rvert p_x\rvert P2_{+}^{-},\frac{1}{2}\rangle=i\langle P1_{-}^{+},\frac{1}{2}\rvert p_y\rvert P2_{+}^{-},-\frac{1}{2}\rangle\\ =-i\langle P1_{-}^{+},-\frac{1}{2}\rvert p_x\rvert P2_{+}^{-},\frac{1}{2}\rangle=P_0\] \[\langle P1_{-}^+,\frac{1}{2}\rvert p_z\rvert P2_{+}^{-},\frac{1}{2}\rangle=-\langle P1_{-}^{+},-\frac{1}{2}\rvert p_z\rvert P2_{+}^{-},-\frac{1}{2}\rangle=Q_0\]

接下来开始考虑微扰,简并微扰的公式如下

\[H_{mm^\prime }^{(0)}=E_m\delta_{mm^\prime }\] \[H_{mm^\prime }^{(1)}=H_{mm^\prime }^\prime\] \[H^{(2)}_{mm^\prime }=\frac{1}{2}\sum_lH^\prime _{ml}H^\prime _{lm^\prime }(\frac{1}{E_m-E_l}-\frac{1}{E_{m'}-E_l})\] \[H^{(3)}_{mm^\prime }=-\frac{1}{2}\sum_{l,m^{''}}[\frac{H^\prime _{ml}H^\prime _{lm^{''}}H^\prime _{m^{''}m^\prime }}{(E_{m^\prime }-E_l)(E_{m^{''}}-E_l)}+\frac{H^\prime _{mm^{''}}H^\prime _{m^{''}l}H^\prime _{lm^\prime }}{(E_m-E_l)(E_{m^{''}}-E_l)}]\\ +\frac{1}{2}\sum_{l,l^\prime }H^\prime _{ml}H^\prime _{ll^\prime }H^\prime _{l^\prime m^\prime }[\frac{1}{(E_m-E_l)(E_m-E_{l^\prime })}+\frac{1}{(E_{m^\prime }-E_l)(E_{m^\prime }-E_{l^\prime })}]\]

这里$m,m^\prime$可以取

\[\rvert P1_{-}^+,1/2\rangle=\rvert 1\rangle,\rvert P2_{+}^{-},1/2\rangle=\rvert 2\rangle,\rvert P1_{-}^+,-1/2\rangle=\rvert 3\rangle,\rvert P2_{+}^{-},-1/2\rangle=\rvert 4\rangle\]

对应的能量为$E_1=E_3,E_2=E_4,E_1 < E_2,l$会遍历除了这四个能带之外的其他能带.

通过简并微扰的到的哈密顿量将会是一些依赖于动量矩阵元$\rvert \Lambda_1,\alpha\rvert\mathbf{p}\rvert\Lambda_2,\beta\rangle$,通过晶体的对称性,这些矩阵元可以被简化.比如,因为晶体存在反演对称,在$\Gamma$点的每个态都具有确定的宇称,因为动量$\mathbf{p}$是奇宇称的,那么当动量矩阵元中的两个态都是相同的宇称的时候,这一项是等于零的(相容性原理).波函数可以通过第一性原理计算,从而就可以计算这些对应的矩阵元素.通过这些矩阵元素和上面简并微扰的计算,就可以的到模型哈密顿量.其中参数的计算如下

\[C_0+M_0=E_1\] \[C_0-M_0=E_2\] \[C_1+M_1=\frac{\hbar^2}{2m_0}+\frac{\hbar^2}{m_0^2}\sum_{\Lambda^{-}}\frac{\rvert Q_{P1^+,\Lambda^{-}}\rvert^2}{E_1-E_{\Lambda^{-},1/2}}\] \[C_2+M_2=\frac{\hbar^2}{2m_0}+\frac{\hbar^2}{m_0^2}\sum_{\Lambda^{-}}(\frac{\rvert P_{P1^+,\Lambda^{-}}\rvert^2}{E_1-E_{\Lambda^{-},-1/2}}+\frac{\rvert M_{P1^+,\Lambda^{-}}\rvert^2}{E_1-E_{\Lambda^{-},\Gamma_4}}+\frac{\rvert N_{P1^+,\Lambda^{-}}\rvert^2}{E_1-E_{\Lambda^{-},\Gamma_5}})\] \[C_1-M_1=\frac{\hbar^2}{2m_0}+\frac{\hbar^2}{m_0^2}\sum_{\Lambda^{-}}\frac{\rvert Q_{\Lambda^+,P2^{-}}\rvert^2}{E_1-E_{\Lambda^{+},1/2}}\] \[C_2-M_2=\frac{\hbar^2k^2}{2m_0}+\frac{\hbar^2}{m_0^2}\sum_{\Lambda^{-}}(\frac{\rvert P_{\Lambda^+,P2^{-}}\rvert^2}{E_1-E_{\Lambda^{+},-1/2}}+\frac{\rvert M_{\Lambda^+,P2^{-}}\rvert^2}{E_1-E_{\Lambda^{+},\Gamma_4}}+\frac{\rvert N_{\Lambda^+,P2^{-}}\rvert^2}{E_1-E_{\Lambda^{+},\Gamma_5}})\] \[A_0=\frac{\hbar}{m_0}P_0\] \[B_0=\frac{\hbar}{m_0}Q_0\] \[R_1-R_2=\frac{\hbar^3}{m_0^3}[\sum_{\Lambda}\frac{\rvert M_{P1^+,\Lambda^{-}}\rvert^2P_{P1^+,P2^{-}}}{(E_{P2^{-}}-E_{\Lambda^{-}})(E_{P1^{+}}-E_{\Lambda^{-}})}]-\sum_{\Lambda_1^{-},\Lambda_2^{+}}M_{P1^+\Lambda_1^{+}}M^{*}_{\Lambda_2^{+}\Lambda_1^{+}}P_{\Lambda_1^{+}P2^{-}}(\frac{1}{(E_{P1^{+}}-E_{\Lambda_1^{-}})(E_{P1^{+}}-E_{\Lambda_2^{+}})}+\frac{1}{(E_{P2^{-}}-E_{\Lambda_1^{-}})(E_{P2^{-}}-E_{\Lambda_2^{+}})})\] \[R_1+R_2=\frac{\hbar^3}{m_0^3}[-\sum_{\Lambda}\frac{\rvert M_{P2^{-},\Lambda^{-}}\rvert^2P_{P1^+,P2^{-}}}{(E_{P2^{-}}-E_{\Lambda^{+}})(E_{P1^{+}}-E_{\Lambda^{+}})}]-\sum_{\Lambda_1^{-},\Lambda_2^{+}}M_{\Lambda_1^{-}\Lambda_2^{+}}M^{*}_{P2^{-}\Lambda_2^{+}}P_{P1^{+}\Lambda_1^{-}}(\frac{1}{(E_{P1^{+}}-E_{\Lambda_1^{-}})(E_{P1^{+}}-E_{\Lambda_2^{+}})}+\frac{1}{(E_{P2^{-}}-E_{\Lambda_1^{-}})(E_{P2^{-}}-E_{\Lambda_2^{+}})})\]

表面态

考虑一个定义在半个空间的哈密顿量模型$z>0$,可以将模型哈密顿量分成两部分

\[\hat{H}=\tilde{H}_0+\tilde{H}_1\] \[\tilde{H}_0\tilde{\epsilon}(k_z)\tilde{M}(k_z)\Gamma_5+B_0\Gamma_4k_z\] \[\tilde{H}_1+C_2k_\parallel^2+M_2k_\parallel^2\Gamma_5+A_)\Gamma_1k_y-\Gamma_2k_x)+H_3\]

这里$\tilde{\epsilon}(k_z)=C_0+C_1k_z^2,\tilde{M}(k_z)M_0+M_1k_z^2$.所有与$k_z$有关的项都包含在$\tilde{H}_0$中,替换$k_z\rightarrow -i\partial_z$并求解本征方程

\[\tilde{H}_0(k_z\rightarrow -i\partial_z)\Psi(z)=E\Psi(z)\]

因为$\Gamma_4=\mathbb{I}\times\tau_2,\Gamma_5=\mathbb{I}\times\tau_3$都是块对角的,哈密顿量同样也是块对角的,本征态的形式为

\[\Psi_\uparrow(z)=\left(\begin{array}{c}\psi_0\\ \mathbf{0}\end{array}\right),\quad \Psi_\downarrow(z)=\left(\begin{array}{c} \mathbf{0}\\ \psi_0\end{array}\right)\]

这里的$\Psi_\uparrow(z),\Psi_\downarrow(z)$是由时间反演联系的.为了得到表面态,$\psi_0$需要满足本征方程

\[(\tilde{\epsilon}(-i\partial_z)+\tilde{M}(-i\partial_z)\tau_3-iB_o\tau_2\partial_z)\psi_0(z)=E\psi_0(z)\]

此时可以忽略$\tilde{\epsilon}$项,上面的本征方程就存在粒子空穴对称,因此可以期待$E=0$本征态的出现,假设波函数为$\psi_0=\phi e^{\lambda z}$,本恒方程简化为

\[(M_0-M_1\lambda^2)\tau_1\phi=B_0\lambda\phi\]

很明显两分量的闭函数$\phi$应该是Pauli矩阵$\tau_1$的本征态,定义$\tau_1\phi_\pm=\pm\phi_\pm$,则上面的方程可以简化成一个关于$\lambda$的二次方程.如果$\lambda$是解$\phi_{+}$的本征值,$-\lambda$是$\phi_{-}$的本征值,波函数可以得到为

\[\phi_0(z)=(ae^{\lambda_1z}+be^{\lambda_2z})\phi_{+}+(ce^{-\lambda_1z}+de^{-\lambda_2z})\phi_{-}\]

本征值$\lambda$满足

\[\lambda_{1,2}=\frac{1}{2M_1}(-B_0\pm\sqrt{4M_0M_1+B_0^2})\]

利用边界条件$\phi(0)=0$以及波函数只存在于$z>0$的区域,从而可以得到$\mathcal{R}(\lambda_{1,2})<0(c=d=0)$或者$\mathcal{R}(\lambda_{1,2})>0(a=b=0)$,从而得到了满足能带反转的条件$M_0M_1<0$.当$B_0/M_1>0\mathcal{R}(\lambda_{1,2})<0$或者$B_0/M_1<0\mathcal{R}(\lambda_{1,2})>0$,对于在$\Gamma$点的表面态波函数为

\[\psi_0(m)=\left\{\begin{array}{c}a(e^{\lambda_1z}-e^{\lambda_2z}),\quad B_0/M_1>0\\ c(e^{-\lambda_1z}-e^{-\lambda_2z}),\quad B_0/M_1<0\end{array}\right.\]

在$\Psi=[\Psi_\uparrow,\Psi_\downarrow]$的子空间中,可以发现

\[\langle\rvert\Gamma_1\rvert\Psi\rangle=\alpha_1\sigma_x,\quad,\langle\rvert\Gamma_2\rvert\Psi\rangle=\alpha_1\sigma_y,\quad,\langle\rvert\Gamma_3\rvert\Psi\rangle=\alpha_1\sigma_z,\quad,\langle\rvert\Gamma_4\rvert\Psi\rangle=0,\\ \langle\rvert\Gamma_5\rvert\Psi\rangle=\alpha_3,\alpha\equiv\langle\psi_0\rvert\tau_1\rvert\psi\rangle,\alpha\equiv=\langle\psi_0\rvert\tau_3\rvert\psi_0\rangle\]

最终可以得到有效哈密顿量的表面态为

\[H_\text{surf}=\tilde{C}_0+\tilde{C}_2k_\parallel^2+\tilde{A}(\sigma_xk_y-\sigma_yk_x)+\tilde{R}(k_{+}^3+k_{-}^3)\sigma_z\\ =(C_0+\alpha_3 M_0)+(C_2+\alpha_3M_2)k_\parallel^2+A_0\alpha_1(\sigma_xk_y-\sigma_yk_x)+\frac{R_1\alpha_1}{2}(k_{+}^3+k_{-}^3)\sigma_z\]

这里的$k_\pm=k_x\pm k_y=k_\parallel e^{\pm i\theta}$.

参考

• 1.Model Hamiltonian for topological insulators
• 2.The $k\cdot p$Method

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。