这里整理一下高阶拓扑的BBH模型的一些拓扑性质的计算,包括边界态,Wilson loop以及Nested Wilson loop计算.
Wilson loop
这个计算没有什么好说的,在其他模型里面也已经做过很多次了,比如BHZ模型Wilson loop计算这篇博客,废话不多说直接上代码
import numpy as np
import matplotlib.pyplot as plt
def Pauli():
s0 = np.array([[1,0],[0,1]])
sx = np.array([[0,1],[1,0]])
sy = np.array([[0,-1j],[1j,0]])
sz = np.array([[1,0],[0,-1]])
return s0,sx,sy,sz
#--------------------------------------------------------------
def hamset(kx,ky):
s0 = np.zeros([2,2],np.complex)
sx = np.zeros([2,2],np.complex)
sy = np.zeros([2,2],np.complex)
sz = np.zeros([2,2],np.complex)
ham = np.zeros([4,4],np.complex)
gamx = 0.5
gamy = 0.5
lamx = 1.0
lamy = 1.0
s0,sx,sy,sz = Pauli()
ham = (gamx + lamx*np.cos(kx))*np.kron(sx,s0) + lamx*np.sin(kx)*np.kron(-sy,sz) + (gamy + lamy*np.cos(ky))*np.kron(-sy,sy) + lamy*np.sin(ky)*np.kron(-sy,sx)
return ham
#--------------------------------------------------------------
def WilsonLoop():
nkx = 100
nky = 100
kxlist = np.linspace(-np.pi, np.pi, nkx)
kylist = np.linspace(-np.pi, np.pi, nky)
anglist = []
for ky in kylist:
wave1 = []
wave2 = []
for kx in kxlist:
eigval, eigvec = np.linalg.eigh(hamset(kx, ky))
if kx != np.pi:
wave1.append(eigvec[:, 0]) # 第一个占据态波函数
wave2.append(eigvec[:, 1]) # 第二个占据态波函数
else:
# 首位波函数相同,消除规范
wave1.append(wave1[0])
wave2.append(wave2[0])
Wan = np.eye(2,dtype=complex)
for i0 in range(nkx - 1):
F = np.zeros((2, 2), dtype = complex)
F[0, 0] = np.dot(wave1[i0 + 1].transpose().conj(), wave1[i0]) # 两个占据态波函数之间的交叠
F[1, 1] = np.dot(wave2[i0 + 1].transpose().conj(), wave2[i0])
F[0, 1] = np.dot(wave1[i0 + 1].transpose().conj(), wave2[i0])
F[1, 0] = np.dot(wave2[i0 + 1].transpose().conj(), wave1[i0])
Wan = np.dot(F, Wan)
eigval, eigvec = np.linalg.eig(Wan)
ang = np.log(eigval)/2/np.pi/1j
for i0 in range(2):
if np.real(ang[i0]) < 0:
ang[i0] += 1
ang = np.sort(ang)
anglist.append(ang.real)
return anglist
#------------------------------------------------
def WilsonLoop2():
nkx = 100
nky = 100
kxlist = np.linspace(-np.pi, np.pi, nkx)
kylist = np.linspace(-np.pi, np.pi, nky)
hn = hamset(0,0).shape[0]
Nocc = int(hn/2)
wave = np.zeros([hn,hn,nkx],np.complex)
anglist = []
for ky in kylist:
ix = 0
for kx in kxlist: # 计算沿着kx方向的Wilson loop
eigval, eigvec = np.linalg.eigh(hamset(kx, ky)) # 求解哈密顿量的本征矢量
if kx != np.pi:
wave[:,:,ix] = eigvec[:,:] # 存储所有的本征波函数,用来后面计算Wilson loop
ix += 1
else:
# 首尾波函数相同,消除规范
wave[:,:,nkx - 1] = wave[:,:,0]
Wan = np.eye(Nocc,dtype = complex)
F = np.zeros((Nocc, Nocc), dtype = complex) # Wannier Hamiltonian
for i0 in range(nkx - 1):
for i1 in range(Nocc): # 直接通过循环,只遍历占据态的波函数
for i2 in range(Nocc):
F[i1,i2] = np.dot(wave[:,i1,i0 + 1].transpose().conj(),wave[:,i2,i0])
Wan = np.dot(F, Wan)
eigval, eigvec = np.linalg.eig(Wan)
ang = np.log(eigval)/(2*np.pi*1j)
for i0 in range(2):
if np.real(ang[i0]) < 0:
ang[i0] += 1
ang = np.sort(ang)
anglist.append(ang.real)
return anglist
#------------------------------------------------------
def main():
a1 = WilsonLoop()
a2 = WilsonLoop2()
fig = plt.figure()
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
ax1.plot(a1)
ax2.plot(a2)
#--------------------------------------------------------
if __name__ == '__main__':
main()
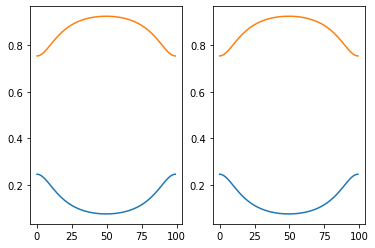
这里采用了两种写代码的方式,第一种就是老老实实按照占据态的计算,而第二种则是将所有都整理到一起,需要用到占据态的时候在直接提取占据态对应的波函数来计算.
边界态
这部分同样没有太多需要讲解的,直接参考快速格林函数方法计算Chern绝缘体边界态这篇博客,直接上代码
import numpy as np
import matplotlib.pyplot as plt
import os
import time
import seaborn as sns
def Pauli():
s0 = np.array([[1,0],[0,1]])
sx = np.array([[0,1],[1,0]])
sy = np.array([[0,-1j],[1j,0]])
sz = np.array([[1,0],[0,-1]])
return s0,sx,sy,sz
#------------------------------------------------
def hamset(ki):
s0 = np.zeros([2,2],np.complex)
sx = np.zeros([2,2],np.complex)
sy = np.zeros([2,2],np.complex)
sz = np.zeros([2,2],np.complex)
H00 = np.zeros([4,4],np.complex)
H01 = np.zeros([4,4],np.complex)
gamx = 0.5
gamy = 0.5
lamx = 1.0
lamy = 1.0
s0,sx,sy,sz = Pauli()
H00 = (gamx + lamx*np.cos(ki))*np.kron(sx,s0) + lamx*np.sin(ki)*np.kron(-sy,sz)
H01 = (gamy + lamy/2.0)*np.kron(-sy,sy) + lamy/(2*1j)*np.kron(-sy,sx)
return H00,H01
# -----------------------------------------------------------------------
def Iteration(omega,ki):
err = 1e-16
eta = 0.01
iternum = 200
# H00 = np.zeros((2,2),np.complex128)
# H01 = np.zeros((2,2),np.complex128)
H00,H01 = hamset(ki)
epsiloni = H00
epsilons = H00
epsilons_t = H00
alphai = H01
betai = H01.T.conjugate()
omegac = omega + eta*1j
# s0,sx,sy,sz = Pauli()
s0 = np.eye(4)
for iter in range(iternum):
g0dem = omegac*s0 - epsiloni
g0 = np.linalg.inv(g0dem)
mat1 = np.dot(alphai,g0)
mat2 = np.dot(betai,g0)
g0 = np.dot(mat1,betai)
epsiloni = epsiloni + g0
epsilons = epsilons + g0
g0 = np.dot(mat2,alphai)
epsiloni = epsiloni + g0
epsilons_t = epsilons_t + g0
g0 = np.dot(mat1, alphai)
alphai = g0
g0 = np.dot(mat2,betai)
betai = g0
real_temp = np.sum(np.concatenate(np.abs(alphai)))
if (real_temp < err):
break
GLLdem = np.dot(omegac,s0) - epsilons
GLL = np.linalg.inv(GLLdem)
# GLL = epsilons
GLL = np.sum(np.concatenate(np.abs(GLL)))
GRRdem = np.dot(omegac,s0) - epsilons_t
GRR = np.linalg.inv(GRRdem)
GRR = np.sum(np.concatenate(np.abs(GRR)))
# GRR = epsilons_t
GBdem = np.dot(omegac,s0) - epsiloni
GB = np.linalg.inv(GBdem)
GB = np.sum(np.concatenate(np.abs(GB)))
# GB = epsiloni
return GLL,GRR,GB
#------------------------------------------------------------
def surface():
nx = 100
max_omg = 3
re = np.zeros((len(range(-nx,nx))**2,5))
con = 0
ix = -1
iy = -1
GLL = np.zeros((len(range(-nx,nx)),len(range(-nx,nx))))
GRR = np.zeros((len(range(-nx,nx)),len(range(-nx,nx))))
GB = np.zeros((len(range(-nx,nx)),len(range(-nx,nx))))
for i0 in range(-nx,nx):
kx = np.pi*i0/nx
for i1 in range(-nx,nx):
omg = max_omg*i1/nx
re1,re2,re3 = Iteration(omg,kx)
re[con,0] = kx
re[con,1] = omg
re[con,2] = re1
re[con,3] = re2
re[con,4] = re3
GLL[iy,ix] = np.log(re1)
GRR[iy,ix] = np.log(re2)
GB[iy,ix] = np.log(re3)
con += 1
iy += 1
ix += 1
iy = 0
# np.savetxt("GLL.dat", [kilist,re1list], fmt="%15.10f")
# np.savetxt("GRR.dat", [kilist,re1list], fmt="%15.10f")
# np.savetxt("GB.dat", [kilist,re1list], fmt="%15.10f")
np.savetxt("density.dat",re , fmt="%15.10f")
return GLL,GRR,GB
#-----------------------------------------------------------------------
def main():
os.chdir(os.getcwd())
tstart = time.time()
GLL,GRR,GB = surface()
tend = time.time()
#print(tend - tstart)
# 绘图
sns.set()
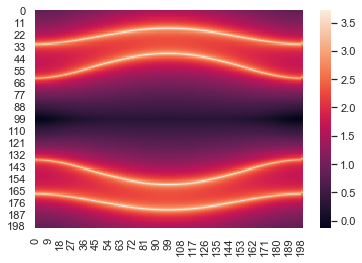
ax = sns.heatmap(GB)
plt.show()
#-----------------------------------------------------------------------
if __name__ == '__main__':
main()
Nested Wilson Loop
关于Nested Wilson loop的计算可以参考Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators 这篇文章,这里主要说一下自己在学习计算的时候踩过的坑。
与计算Wilson loop相同,这里最主要的仍然是找到一个Wannier band basis,也就是文章的中的公式
\[\rvert w_{x,\mathbf{k}}^j\rangle=\sum_{n=1}^\text{Nocc}\rvert u^n_\mathbf{k}\rangle[v_{x,\mathbf{k}}^j]^n\]其实在做计算的时候,最让人困扰的不过是公式中的一大堆符号对应的到底是什么,这里就来讲这个公式拆解开,一步一步的讲清楚里面的含义。这里假设你已经知道为什么要计算Nested Wilson loop, 我在这里就简单的阐述一下。首先要是体系的Wilson loop计算对应的Wannier哈密顿量的能带是有能隙的,也就是说你的体系是4带模型,那么当占据态是2条能带的时候,每个占据态能带会对应着一个Wannier center, 比如BHZ模型的两条占据态能带对应的Wannier band就是相互交叉的,而且因为Wilson loop与边界态之间的拓扑等价性,TI是有边界态的,所以其对应的Wilson loop在形状上就与边界态类似。而对于高阶拓扑相, 首先就是要使得边界态打开能隙,那么相对应的就是其Wilson loop计算得到的Wannier center随着某个动量参数的演化是不会相互交叉的,这一点在上面BBH模型中已经计算过了,所以此时就可以对某一个单独的Wannier band 计算它的Nested Wilson loop,所以首先第一步就是必须要明白什么样的情况下,是需要计算体系的Nested Wilson loop。
这里的$\sum_{n=1}^\text{Nocc}$不用讲太多,是需要对占据态进行求和,但是这个$n$其实表示的只是说哈密顿量的占据态,也就是说对于$\rvert u^n_\mathbf{k}\rangle$而言,这是哈密顿量的占据态波函数,$n$表示占据态其实是对$\rvert u^n_\mathbf{k}\rangle$ 而言的,虽然$[v_{x,\mathbf{k}}^j]^n$中同样存在这个$n$,但是在这个地方$n$代表的不是占据态,在这里$j$代表的才是你选择的是哪一个Wannier band来计算其对应的Nested Wilson loop,也就是这里$j$代表的是你选择的是那个占据的Wannier band,而$n$在这里 表示的是一个Wannier哈密顿量本征矢量的第$n$个分量。假如$H_\text{Wann}$是Wannier哈密顿量,其满足
\[H_\text{Wann}\rvert v_\mathbf{k}\rangle=E\rvert v_\mathbf{k}\rangle\]那么这里的$[v_{x,\mathbf{k}}^j]^n$表示的就是这个本征矢量的第$n$个分量,$j$则表示你选择是哪个本征值对应的本征矢量,也就是选择了哪一个Wannier band。这里的$x$则表示你在做Wilson loop的时候,是沿着哪个方向进行的,即就是讲上面公式中的$H_\text{Wann}$替换成你 构建的那个Wilson loop的哈密顿量就可以。
至于$\rvert u^n_\mathbf{k}\rangle$就很简单了,它表示的就是你的哈密顿量的本征态,当然了在计算的时候,还是要选择正确的占据态才可以。下面直接上代码,在其中同样做了注释
import numpy as np
import matplotlib.pyplot as plt
import os
import time
#--------------------------------------------------
def hamset(kx,ky):
# 构建模型哈密顿量
gamx = 0.5 # hopping inside one unit cell
lamx = 1 # hopping between unit cells
gamy = gamx
lamy = lamx
xsyb1 = 0.000000000000 # default (not breaking): zero
xsyb2 = 1.0000000000001 # default (not breaking): unity
ysyb1 = 0.000000000000 # default (not breaking): zero
ysyb2 = 1.000000000000 # default (not breaking): unity
ham = np.zeros((4, 4), dtype = complex)
ham[0, 0] = xsyb1
ham[1, 1] = ysyb1
ham[2, 2] = ysyb1
ham[3, 3] = xsyb1
ham[0, 2] = (gamx + lamx * np.exp(1j * kx)) * ysyb2
ham[1, 3] = gamx + lamx * np.exp(-1j * kx)
ham[0, 3] = gamy + lamy * np.exp(1j * ky)
ham[1, 2] = (-gamy - lamy * np.exp(-1j * ky)) * xsyb2
ham[2, 0] = np.conj(ham[0, 2])
ham[3, 1] = np.conj(ham[1, 3])
ham[3, 0] = np.conj(ham[0, 3])
ham[2, 1] = np.conj(ham[1, 2])
return ham
#-------------------------------------------------------------
def Wilson_kx(kx):
# 在给定kx的情况下,计算沿着ky方向上的Wilson loop
# 相当于是讲原本计算Wilson loop的方法,现在拆解成每个离散的点
nky = 100
hn = hamset(0,0).shape[0] # 获取哈密顿量的维度,方便构建占据态
Nocc = int(hn/2)
wave = np.zeros((hn,hn,nky),dtype = complex) # 存储所有ki点上的本征波函数
kylist = np.linspace(-np.pi, np.pi, nky)
# 构建沿着y方向的Wilson loop,此时给定一个kx值进行一次Wilson loop计算
ix = 0
for ky in kylist: # 计算沿着kx方向的Wilson loop
eigval, eigvec = np.linalg.eigh(hamset(kx, ky)) # 求解哈密顿量的本征矢量
if ky != np.pi:
wave[:,:,ix] = eigvec[:,:] # 存储所有的本征波函数,用来后面计算Wilson loop
ix += 1
else:
# 首尾波函数相同,消除规范
wave[:,:,nky - 1] = wave[:,:,0]
ix += 1
# 利用沿着ky方向计算的波函数来构建Wannier hamiltonian
Wan = np.eye(Nocc,dtype = complex)
F = np.zeros((Nocc, Nocc), dtype = complex) # Wannier Hamiltonian
for i0 in range(nky - 1):
for i1 in range(Nocc): # 直接通过循环,只遍历占据态的波函数,在设定化学势为零的时候,占据态是能带数的一半
for i2 in range(Nocc): # 不同占据态在相邻kx格点上的波函数交叠
F[i1,i2] = np.dot(wave[:,i1,i0 + 1].transpose().conj(),wave[:,i2,i0])
Wan = np.dot(F, Wan)
eigval, eigvec = np.linalg.eig(Wan) # 这里Wannier 哈密顿量并不是厄米的,所以求解得到的本征值的顺序并不一定就是按顺序排列的
mux = np.log(eigval)/(2*np.pi*1j) # 从Wannier哈密顿量中计算Wannier center
wannier_vec1 = eigvec[:, np.argsort(np.real(mux))[0]] # 按照特定的顺序排列本征矢量
wannier_vec2 = eigvec[:, np.argsort(np.real(mux))[1]]
# 返回两个Wannier band在确定kx下的本征矢量,因为对于一个四带模型,这里的占据态的数目是2,所以必然存在两个Wannier band
return wannier_vec1,wannier_vec2
#---------------------------------------------------------------------------------------------------------
def Wilson_ky(ky):
# 在给定kx的情况下,计算沿着ky方向上的Wilson loop
# 相当于是讲原本计算Wilson loop的方法,现在拆解成每个离散的点
nkx = 100
hn = hamset(0,0).shape[0] # 获取哈密顿量的维度,方便构建占据态
Nocc = int(hn/2)
wave = np.zeros((hn,hn,nkx),dtype = complex) # 存储所有ki点上的本征波函数
kxlist = np.linspace(-np.pi, np.pi, nkx)
# 构建沿着y方向的Wilson loop,此时给定一个kx值进行一次Wilson loop计算
ix = 0
for kx in kxlist: # 计算沿着kx方向的Wilson loop
eigval, eigvec = np.linalg.eigh(hamset(kx, ky)) # 求解哈密顿量的本征矢量
if kx != np.pi:
wave[:,:,ix] = eigvec[:,:] # 存储所有的本征波函数,用来后面计算Wilson loop
ix += 1
else:
# 首尾波函数相同,消除规范
wave[:,:,nkx - 1] = wave[:,:,0]
ix += 1
# 利用沿着ky方向计算的波函数来构建Wannier hamiltonian
Wan = np.eye(Nocc,dtype = complex)
F = np.zeros((Nocc, Nocc), dtype = complex) # Wannier Hamiltonian
for i0 in range(nkx - 1):
for i1 in range(Nocc): # 直接通过循环,只遍历占据态的波函数
for i2 in range(Nocc):
F[i1,i2] = np.dot(wave[:,i1,i0 + 1].transpose().conj(),wave[:,i2,i0])
Wan = np.dot(F, Wan)
eigval, eigvec = np.linalg.eig(Wan) # 这里Wannier 哈密顿量并不是厄米的,所以求解得到的本征值的顺序并不一定就是按顺序排列的
mux = np.log(eigval)/(2*np.pi*1j) # 从Wannier哈密顿量中计算Wannier center
wannier_vec1 = eigvec[:, np.argsort(np.real(mux))[0]] # 按照特定的顺序排列本征矢量(这里的顺序是从小到大排列)
wannier_vec2 = eigvec[:, np.argsort(np.real(mux))[1]]
return wannier_vec1,wannier_vec2 # 返回两个Wannier band在确定ky下的本征矢量
#---------------------------------------------------------------------------------------------------------
def Nested_Wilson_loop_kx():
nkx = 100 # 计算Nested Wilson loop时撒点的数目
nky = 100
hn = hamset(0,0).shape[0] # 获取哈密顿量的维度,方便构建占据态
Nocc = int(hn/2) # 占据态能带数目
kxlist = np.linspace(-np.pi, np.pi, nkx)
kylist = np.linspace(-np.pi, np.pi, nky)
wave = np.zeros((hn,hn,nky),dtype = complex)
pmulist = []
for kx in kxlist:
ix = 0 # 这里的ix用来索引ky,将所有固定kx下面的沿ky方向的波函数都存储起来
for ky in kylist: # 沿着一个方向遍历动量
eigval,eigvec = np.linalg.eigh(hamset(kx,ky)) # 求解哈密顿量的本征矢量和本征值
if ky != np.pi:
wave[:,:,ix] = eigvec[:,:] # 将沿着ky方向的所有本征波函数存储
ix += 1
else:
wave[:,:,nky - 1] = wave[:,:,0] # 在边界上保证波函数首尾相接
ix += 1
#------------------------------------------------------------------
i0 = 0
wmu = np.zeros((4,nky),dtype = complex) # 用来构建新的Wannier basis
for ky in kylist:
if ky != np.pi:
wann_v1,wann_v2 = Wilson_ky(ky) # 给定一个ky,沿着kx方向做完Wilson loop,得到两个Wannier band对应的本征矢量
# 将两个占据态的都进行计算,哈密顿量的每个占据态于Wannier band占据态的每个分量进行相乘然后求和(这里的本征值是按照顺序排列的,所以只使用了占据态)
wmu[:,i0] = wave[:,0,i0]*wann_v1[0] + wave[:,1,i0]*wann_v1[1]
else:
wmu[:,nky - 1] = wmu[:,0] # 在新的Wannier basis下,波函数首尾相接
i0 += 1
#--------------------------------------
# 对新的Wannier basis构建的函数计算Wilson loop,只不过此时的可能就是一个复数相乘,因为只有一条带,那么自然就不会是个矩阵
wan = 1
for i0 in range(nkx - 1):
F0 = np.dot(wmu[:,i0 + 1].T.conj(),wmu[:,i0])
wan = F0*wan
pmu = np.log(wan)/(2*1j*np.pi)
if np.real(pmu) < 0:
pmu += 1
pmulist.append(pmu.real)
return kxlist,pmulist
#---------------------------------------------------------------------------------------------------------
def Nested_Wilson_loop_ky():
nkx = 100 # 计算Nested Wilson loop时撒点的数目
nky = 100
hn = hamset(0,0).shape[0] # 获取哈密顿量的维度,方便构建占据态
Nocc = int(hn/2) # 占据态能带数目
kxlist = np.linspace(-np.pi, np.pi, nkx)
kylist = np.linspace(-np.pi, np.pi, nky)
wave = np.zeros((hn,hn,nky),dtype = complex) # 存储哈密顿量对应的本征波函数
pmulist = []
for ky in kylist:
ix = 0 # 这里的ix用来索引ky,将所有固定kx下面的沿ky方向的波函数都存储起来
for kx in kxlist: # 沿着一个方向遍历动量
eigval,eigvec = np.linalg.eigh(hamset(kx,ky)) # 求解哈密顿量的本征矢量和本征值
if kx != np.pi:
wave[:,:,ix] = eigvec[:,:] # 将沿着ky方向的所有本征值对应的本征波函数存储
ix += 1
else:
wave[:,:,nky - 1] = wave[:,:,0] # 在边界上保证波函数首尾相接
ix += 1
#------------------------------------------------------------------
i0 = 0
wmu = np.zeros((4,nkx),dtype = complex) # 用来构建新的Wannier basis
for kx in kylist:
if kx != np.pi:
wann_v1,wann_v2 = Wilson_kx(kx) # 给定一个ky,沿着kx方向做完Wilson loop,得到两个Wannier band对应的本征矢量
# 将两个占据态的都进行计算,哈密顿量的每个占据态于Wannier band占据态的每个分量进行相乘然后求和(这里的本征值是按照顺序排列的,所以只使用了占据态)
wmu[:,i0] = wave[:,0,i0]*wann_v1[0] + wave[:,1,i0]*wann_v1[1]
else:
wmu[:,nky - 1] = wmu[:,0] # 在新的Wannier basis下,波函数首尾相接
i0 += 1
#--------------------------------------
# 对新的Wannier basis构建的函数计算Wilson loop,只不过此时的可能就是一个复数相乘,因为只有一条带,那么自然就不会是个矩阵
wan = 1
for i0 in range(nky - 1):
F0 = np.dot(wmu[:,i0 + 1].T.conj(),wmu[:,i0])
wan = F0*wan
pmu = np.log(wan)/(2*1j*np.pi)
if np.real(pmu) < 0:
pmu += 1
pmulist.append(pmu.real)
return kylist,pmulist
#-------------------------------------------------------
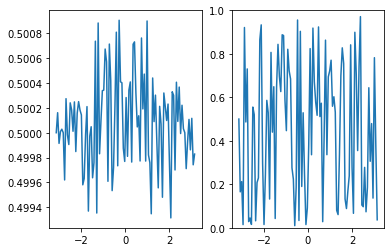
def main1():
x1,y1 = Nested_Wilson_loop_kx()
x2,y2 = Nested_Wilson_loop_ky()
fig = plt.figure()
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
ax1.plot(x1,y1)
ax2.plot(x2,y2)
ax1.ylim(0,1)
ax2.ylim(0,1)
#-------------------------------------------------------
def main2():
x,y = Nested_Wilson_loop_kx()
# x,y = Nested_Wilson_loop_ky()
plt.plot(x,y)
plt.ylim(0,1)
#-------------------------------------------------------
if __name__ == '__main__':
os.chdir(os.getcwd()) # 更改工作目录到当前文件夹
tstart = time.time() # 获取系统时间
main1()
tend = time.time()
print("Consted time is %.5f" % (tend - tstart))
完整的代码可以点击这里下载.
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |