这里整理一下如何通过Wannier band basis的高对称点对称性本征值来计算体系的电四极矩。想使用这个方法的主要原因是在计算Nested Wilson loop得到电四极矩的时候,如果占据态能带存在简并,这个时候直接利用公式计算会得到不稳定的结果,暂时也没找到解决的办法,所以换个方法来计算电四极矩,而且发现利用对称性指标计算效率更高。
模型
这里研究我最熟悉的模型,将BHZ模型和$d$波超导体结合起来,这早期实现高阶拓扑超导体的方案之一,其模型为
\[\begin{align} H(\mathbf{k})&=(m_0-t_x\cos k_x-t_y\cos k_y)\sigma_z\tau_z+A_x\sin k_x\sigma_xs_z+A_y\sin k_y\sigma_y\tau_z\\ & +\Delta_0(\cos k_x-\cos k_y)s_y\tau_y-\mu\tau_z \end{align}\]这个是一个体态电四极矩贡献的高阶拓扑相(这里我就不解释为什么了,感兴趣可以和我讨论)。它具有$x$和$y$方向的Mirror对称性
\[\begin{align} &\mathcal{M}_x=is_y\sigma_x\tau_y\\ &\mathcal{M}_y=is_x\sigma_y\tau_x\\ \end{align}\]哈密顿量在Mirror对称操作下满足
\[\begin{align} &\mathcal{M}_xH(k_x,k_y)\mathcal{M}_x^{-1}=H(-k_x,k_y)\\ &\mathcal{M}_yH(k_x,k_y)\mathcal{M}_y^{-1}=H(k_x,-k_y)\\ \end{align}\]除此之外系统还存在inverison对称性
\[\mathcal{P}H(\mathbf{k})\mathcal{P}^{-1}=H(\mathbf{k})\qquad \mathcal{P}=\sigma_z\]当体系存在Mirror对称性和空间反演对称性之后,其Wannier sector的极化满足(可以参考Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators这篇文章)
\[p_{y}^{\nu_{x}^{+}} \stackrel{\mathcal{I}}{=}-p_{y}^{\nu_{x}^{-}},\qquad p_{y}^{\nu_{x}^{+}} \stackrel{\mathcal{M}_{x}}{=} p_{y}^{\nu_{x}^{-}},\qquad p_{y}^{\nu_{x}^{\pm}} \stackrel{\mathcal{M}_{y}}{=}-p_{y}^{\nu_{x}^{\pm}}\]所以,如果存在$\mathcal{M}_x,\mathcal{M}_y,\mathcal{P}$的时候,$p_y^{\theta_x^{\pm}}$一定会是量子化的
\[\begin{align} p^{\nu^\pm_x}_y, p^{\nu^\pm_y}_x \stackrel{M_x,M_y}{=} 0 \text{ or } 1/2. \end{align}\]此时可以通过对称操作在高对称点的本征值来计算Wannier sector的极化(参考Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators),此时Wannier band basis(参考Nested Wilson loop)满足
\[\begin{align} \hat{M}_y \rvert w^\pm_{x,(k_x,k_y)}\rangle=\alpha^{\pm}_{M_y}(k_x,k_y)\rvert w^\pm_{x,(k_x,-k_y)}\rangle \end{align}\]这里$\alpha^{\pm}_{M_y}(k_x,k_y)$是$U(1)$的位相。
在reflection不变动量点$k_{y}=0 \text{ 和 }\pi$上,$\alpha^{\pm}_{M_y}(k_x, k_{y})$ 是 $\rvert w^\pm_{x,\bf k}\rangle$ 在 $(k_x,k_{*y})$reflection表示的本征值,对spinless的系统它的取值为$\pm 1$,对于spinfull的系统,取值为$\pm i$。
所以如果在 $k_{y} = 0$ 和 $k_{y} = \pi$表示有相同的本征值,那么Wannier sector就是平庸的,如果具有不同的值,那么Wannier sector就是非平庸的。所以在一个reflection对称的绝缘体中,Wannier sector极化可以通过下面的表达式计算
\[\begin{align} \text{exp}\left\{i2\pi p^{\nu^\pm_x}_y\right\} = \alpha^{\pm}_{M_y}(k_x,0) \alpha^{\pm\ast}_{M_y}(k_x,\pi), \end{align}\]这里的$*$表示复共轭操作。Wannier sector可以取量子化的值 \(\begin{align} p^{\nu^\pm_x}_y \stackrel{M_y}{=} \begin{cases} 0 & \text{if trivial}\\ 1/2 & \text{if non-trivial} \end{cases}.\nonumber \end{align}\)
而体态的电四极矩$Q_{xy}$可以表示为
\[Q_{xy}=2p_y^{\nu_x^\pm}p_x^{\nu_y^\pm}\]通过上面的分析可以看到,只要在Wannier band basis上计算得到reflection对称操作的本征值,就可以得到体系的电四极矩。
对于高阶拓扑超导体的模型
\[\begin{align} H(\mathbf{k})&=(m_0-t_x\cos k_x-t_y\cos k_y)\sigma_z\tau_z+A_x\sin k_x\sigma_xs_z+A_y\sin k_y\sigma_y\tau_z\\ & +\Delta_0(\cos k_x-\cos k_y)s_y\tau_y-\mu\tau_z \end{align}\]可以知道的是,只要正常态处于拓扑相,那么在$d$波电子配对的情况下就一定会实现高阶拓扑超导体,选择一组参数
\[t_x=t_y=A_x=A_y=1,\Delta_0=0.5,\mu=0\]那么只要$m_0\in(-2,2)$的区间内,那么体系就会是高阶拓扑超导体,相对应的电四极矩就是$1/2$。下面直接上程序进行计算
Mirror eigenvals
# 计算mirror不变点上Wannier 能带对应的镜面本征值
@everywhere using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles,Printf,Arpack
#-------------------------------------------------------------------------------
@everywhere function pauli()
# 构建Pauli矩阵
hn::Int64 = 2
g0 = zeros(ComplexF64,hn,hn)
gx = zeros(ComplexF64,hn,hn)
gy = zeros(ComplexF64,hn,hn)
gz = zeros(ComplexF64,hn,hn)
#---------------
g0[1,1] = 1
g0[2,2] = 1
gx[1,2] = 1
gx[2,1] = 1
gy[1,2] = -im
gy[2,1] = im
gz[1,1] = 1
gz[2,2] = -1
return g0,gx,gy,gz
end
#---------------------------------------------------------------
@everywhere function hamset(kx::Float64,ky::Float64,m0::Float64)::Matrix{ComplexF64}
# m0::Float64 = 1.
hn::Int64 = 8
tx::Float64 = 1.0
ty::Float64 = 1.0
ax::Float64 = 1.0
ay::Float64 = 1.0
d0::Float64 = 0.
dx::Float64 = 0.5
dy::Float64 = -dx
mu::Float64 = 0.0
ham = zeros(ComplexF64,hn,hn)
s0,sx,sy,sz = pauli()
g1 = kron(s0,sz,sz)
g2 = kron(sz,sx,s0)
g3 = kron(s0,sy,sz)
g4 = kron(sy,s0,sy) # pairing
g5 = kron(s0,s0,sz) # chemical potential
ham = (m0 - tx*cos(kx) - ty*cos(ky))*g1 + ax*sin(kx)*g2 + ay*sin(ky)*g3 + (d0 + dx*cos(kx) + dy*cos(ky))*g4 - mu*g5
return ham
end
#----------------------------------------------------------------------------------
@everywhere function mirror()
# 构造镜面操作算符
s0,sx,sy,sz = pauli()
# mx = kron(sx,sx,sx) # x方向镜面操作
# my = kron(sx,sy,sx) # y方向镜面操作
mx = im*kron(sy,sx,sy) # x方向镜面操作
my = im*kron(sx,sy,sx) # y方向镜面操作
return mx,my
end
#--------------------------------------------------------------------------------------
@everywhere function Wilsonkx(ky::Float64,m0::Float64)
nk::Int64 = 100
hn::Int64 = size(hamset(0.0,0.0,m0))[1]
Nocc::Int64 = Int(hn/2)
wave = zeros(ComplexF64,hn,hn,nk)
wan = zeros(ComplexF64,Nocc,Nocc)
F0 = zeros(ComplexF64,Nocc,Nocc)
vec2 = zeros(ComplexF64,Nocc,Nocc) # 重新排列顺序后Wannier Hamiltonian的本征矢量
klist = range(0, 2*pi, length = nk)
for ix in 1:nk
kx = klist[ix]
val,vec = eigen(hamset(ky,kx,m0))
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nk] = wave[:,:,1] # 波函数首尾相接
for i1 in 1:Nocc
F0[i1,i1] = 1
end
for i1 in 1:nk - 1
for i2 in 1:Nocc
for i3 in 1:Nocc
wan[i2,i3] = wave[:,i2,i1 + 1]' * wave[:,i3,i1] # 计算Berry联络
end
end
sv1 = svd(wan)
wan = sv1.U * sv1.Vt
F0 = wan * F0 # 构造Wannier 哈密顿量
end
val,vec = eigen(F0)
for i0 in 1:Nocc
vec2[:,i0] = vec[:,sortperm(map(angle,val))[i0]] # 对求解得到的本征矢量按照本征值大小排列
end
return vec2 # 给出所有Wannier 本征值对应的本征态
end
#-------------------------------------------------------------------------------------
@everywhere function Wilsonky(ky::Float64,m0::Float64)
nk::Int64 = 100
hn::Int64 = size(hamset(0.0,0.0,m0))[1]
Nocc::Int64 = Int(hn/2)
wave = zeros(ComplexF64,hn,hn,nk)
wan = zeros(ComplexF64,Nocc,Nocc)
F0 = zeros(ComplexF64,Nocc,Nocc)
vec2 = zeros(ComplexF64,Nocc,Nocc) # 重新排列顺序后Wannier Hamiltonian的本征矢量
klist = range(0, 2*pi, length = nk)
for ix in 1:nk # 固定ky,沿着kx方向计算Wilson loop
kx = klist[ix]
val,vec = eigen(hamset(kx,ky,m0))
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nk] = wave[:,:,1] # 波函数首尾相接
for i1 in 1:Nocc
F0[i1,i1] = 1
end
for i1 in 1:nk - 1
for i2 in 1:Nocc
for i3 in 1:Nocc
wan[i2,i3] = wave[:,i2,i1 + 1]' * wave[:,i3,i1] # 计算Berry联络
end
end
sv1 = svd(wan)
wan = sv1.U * sv1.Vt
F0 = wan * F0 # 构造Wannier 哈密顿量
end
val,vec = eigen(F0) # 对求解得到的本征矢量按照本征值大小排列
for i0 in 1:Nocc
vec2[:,i0] = vec[:,sortperm(map(angle,val))[i0]] # 按照顺序对本征态进行排列
end
return vec2 # 给出所有Wannier 本征值对应的本征态
end
#------------------------------------------------------------------------------------
@everywhere function Nestedkx(m0::Float64,kx::Float64,ky::Float64)
# 对应的是y方向上的Nested Wilson loop
hn::Int64 = size(hamset(0.0,0.0,m0))[1] # 直接通过哈密顿量来获取其维度,程序具有通用性
Nocc::Int64 = Int(hn/2) # 获取占据态的数量
wann_vec = Wilsonkx(kx,m0) # ky 方向已经被积掉
val,vec = eigen(hamset(kx,ky,m0))
wmu = zeros(ComplexF64,Nocc,hn)
for i3 in 1:Nocc # 遍历Wannier sector中的每一个Wannier 能带
for i4 in 1:Nocc # 遍历Wannier 本征态中的每个分量
wmu[i3,:] += vec[:,i4] * wann_vec[i4,i3]
end
end
return wmu # 得到每个Wannier能带对应的新的Wannier basis
end
#-----------------------------------------------------------------------
@everywhere function Nestedky(m0::Float64,kx::Float64,ky::Float64)
# 对应的是x方向上的Nested Wilson loop
hn::Int64 = size(hamset(0.0,0.0,m0))[1] # 直接通过哈密顿量来获取其维度,程序具有通用性
Nocc::Int64 = Int(hn/2) # 获取占据态的数量
wann_vec = Wilsonky(ky,m0) # Wilson loop的本征态
val,vec = eigen(hamset(kx,ky,m0)) # 哈密顿量本征态
wmu = zeros(ComplexF64,Nocc,hn) # 用来构建新的Wannier basis
for i3 in 1:Nocc # 遍历Wannier sector中的每一个Wannier 能带
for i4 in 1:Nocc # 遍历Wannier 本征态中的每个分量
wmu[i3,:] += vec[:,i4] * wann_vec[i4,i3]
end
end
return wmu # 得到每个Wannier能带对应的新的Wannier basis
end
#------------------------------------------------
@everywhere function mirroreigval(m0::Float64,kx::Float64,ky::Float64)
# m0::Float64 = 1.5
hn::Int64 = size(hamset(0.0,0.0,m0))[1] # 直接通过哈密顿量来获取其维度,程序具有通用性
Nocc::Int64 = Int(hn/2) # 获取占据态的数量
# kx::Float64 = 0
# ky::Float64 = pi
re1 = zeros(Float64,Nocc)
re2 = zeros(Float64,Nocc)
mux = Nestedkx(m0,kx,ky)
muy = Nestedky(m0,kx,ky)
mx,my = mirror()
for i0 in 1:Nocc
re1[i0] = imag(mux[i0,:]' * mx * mux[i0,:]) # Mirror-Y 操作本征值
re2[i0] = imag(muy[i0,:]' * my * muy[i0,:]) # Mirror-X 操作本征值
end
return re1,re2
end
#--------------------------------------------------
@everywhere function m0chnage(m0list,kx,ky)
hn::Int64 = size(hamset(0.0,0.0,1.0))[1] # 直接通过哈密顿量来获取其维度,程序具有通用性
Nocc::Int64 = Int(hn/2) # 获取占据态的数量
r1list = zeros(length(m0list),Nocc)
r2list = zeros(length(m0list),Nocc)
i0 = 1
for m0 in m0list
r1list[i0,:] = mirroreigval(m0,kx,ky)[1]
r2list[i0,:] = mirroreigval(m0,kx,ky)[2]
i0 += 1
end
re1 = (r1list[:,1] + r1list[:,2])/2
re2 = (r2list[:,1] + r2list[:,2])/2
return re1,re2
end
#-------------------------------------------------
@everywhere function phasex(m0list)
kx = 0.0
ky = 0.
re1,re2 = m0chnage(m0list,kx,ky)
kx = pi*1.0
ky = 0.
re3,re4 = m0chnage(m0list,kx,ky)
mxlist = zeros(Float64,length(m0list))
for i0 in 1:length(m0list)
mxlist[i0] = sign(re1[i0] * re3[i0])
end
fn1 = "mx-dw.dat"
f1 = open(fn1,"w")
x0 = (a->(@sprintf "%3.2f" a)).(m0list)
y0 = (a->(@sprintf "%7.5f" a)).(mxlist)
writedlm(f1,[x0 y0],'\t')
close(f1)
end
#-------------------------------------------------
@everywhere function phasey(m0list)
kx = 0.0
ky = 0.
re1,re2 = m0chnage(m0list,kx,ky)
kx = 0.0
ky = 1.0*pi
re3,re4 = m0chnage(m0list,kx,ky)
mylist = zeros(Float64,length(m0list))
for i0 in 1:length(m0list)
mylist[i0] = sign(re2[i0] * re4[i0])
end
fn1 = "my-dw.dat"
f1 = open(fn1,"w")
x0 = (a->(@sprintf "%3.2f" a)).(m0list)
y0 = (a->(@sprintf "%7.5f" a)).(mylist)
writedlm(f1,[x0 y0],'\t')
close(f1)
end
#-----------------------------------------------
@everywhere function main()
m0list = -4:0.1:4
phasex(m0list)
phasey(m0list)
end
#--------------------------------------------------
@time main()
这个程序就是计算了Wannier band basis下面,在每一个$m_0$下面的镜面操作的本征值,下面再通过对这些本征值的分析来得到电四极矩。程序的思路就是判断在哪些参数区间内,在$0$和$\pi$位置处的本征值是相反的,而且此时要求一定要在$\mathcal{M}_x$和$\mathcal{M}_y$都要在参数区间内反号,才能实现高阶拓扑相
from telnetlib import X3PAD
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#---------------------------------------------------------
def mirrorval(cont):
# 单独画出每个以文件中的数据
#da1 = "m" + str(cont) + "-pro-ox" + ".dat"
#da2 = "m" + str(cont) + "-pro-oy" + ".dat"
da1 = "mx-dw.dat"
da2 = "my-dw.dat"
picname = "mirrorval-" + str(cont) + ".png"
os.chdir(os.getcwd())# 确定用户执行路径
x0 = []
y0 = []
with open(da1) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 3:
ldos = [float(x) for x in f1.strip().split()]
x0.append(ldos[0])
y0.append(ldos[1])
y0 = np.array(y0)
plt.figure(figsize=(10,8))
#-------------------------
# 颜色填充
x1 = np.linspace(-4,0,50)
x2 = np.linspace(0,8,50)
x3 = np.linspace(8,10,50)
y1 = 1.5 + np.sqrt(x1**2*0)
y2 = -1.5 + np.sqrt(x1**2*0)
# plt.fill_between(x1,y2,y1,color = "lightblue", alpha = 0.3)
# plt.fill_between(x2,y2,y1,color = "pink",alpha = 0.3)
# plt.fill_between(x3,y2,y1,color = "lightblue", alpha = 0.3)
#----------------------------------------------------------------
plt.scatter(x0, y0, s = 30, color = 'lightskyblue', label = "$a_{M_x}(0)a^*_{M_x}(\pi)$", marker = "^")
x1 = []
y1 = []
with open(da2) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 3:
ldos = [float(x) for x in f1.strip().split()]
x1.append(ldos[0])
y1.append(ldos[1])
y1 = np.array(y1)
# print(y0)
# sc = plt.scatter(x0, y0, c = z1, s = 2,vmin = 0, vmax = 1, cmap="magma")
plt.scatter(x1, y1, s = 30, color = 'deeppink', label = "$a_{M_y}(0)a^*_{M_y}(\pi)$", marker = "D" )
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 40,
}
font3 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 20,
}
plt.xlim(np.min(x1),np.max(x1))
plt.ylim(-1.5,1.5)
plt.xlabel("$m_0$",font2)
plt.yticks([-1,0.,1],fontproperties='Times New Roman', size = 40)
plt.xticks([np.min(x1),-1,0,2,4,np.max(x1)],fontproperties='Times New Roman', size = 40)
plt.legend(loc = 'upper left', bbox_to_anchor=(0.0,0.8), shadow = True, prop = font3, markerscale = 1, borderpad = 0.1)
#plt.text(x = 0.6,y = 0.7,s = 'MCM', fontdict=dict(fontsize=20, color='black',family='Times New Roman'))
#plt.text(x = 0.1,y = 0.7,s = 'NSC', fontdict=dict(fontsize=20, color='black',family='Times New Roman'))
# plt.vlines(x = 0, ymin = -1.5, ymax = 1.5,lw = 3.0, colors = 'black', linestyles = '--')
plt.vlines(x = 2, ymin = -1.5, ymax = 1.5,lw = 3.0, colors = 'black', linestyles = '--')
plt.vlines(x = -2, ymin = -1.5, ymax = 1.5,lw = 3.0, colors = 'black', linestyles = '--')
plt.savefig(picname, dpi = 100, bbox_inches = 'tight')
plt.close()
#------------------------------------------------------------
def qxy(cont):
# 通过Mx和Mx共同来决定电四极矩,这才是正确的结果
da1 = "mx-dw.dat"
da2 = "my-dw.dat"
picname = "Qxy-" + str(cont) + ".png"
os.chdir(os.getcwd())# 确定用户执行路径
x0 = []
y0 = []
with open(da1) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 3:
ldos = [float(x) for x in f1.strip().split()]
x0.append(ldos[0])
y0.append(ldos[1])
plt.figure(figsize=(8,8))
#-------------------------
# 颜色填充
x1 = np.linspace(-4,0,50)
x2 = np.linspace(0,8,50)
x3 = np.linspace(8,10,50)
y1 = 1 + np.sqrt(x1**2*0)
y2 = -1 + np.sqrt(x1**2*0)
# plt.fill_between(x1,y2,y1,color = "lightblue", alpha = 0.3)
# plt.fill_between(x2,y2,y1,color = "pink",alpha = 0.3)
# plt.fill_between(x3,y2,y1,color = "lightblue",alpha = 0.3)
#----------------------------------------------------------------
y0 = np.array(y0)
# plt.scatter(x0, y0, s = 30, color = 'lightskyblue', label = "$a_{M_x}(0)a_{M_x}(\pi)$", marker = "x")
x1 = []
y1 = []
with open(da2) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 3:
ldos = [float(x) for x in f1.strip().split()]
x1.append(ldos[0])
y1.append(ldos[1])
y1 = np.array(y1)
# print(y0)
# sc = plt.scatter(x0, y0, c = z1, s = 2,vmin = 0, vmax = 1, cmap="magma")
# plt.scatter(x1, y1, s = 30, color = 'deeppink', label = "$a_{M_y}(0)a_{M_y}(\pi)$", marker = "+" )
re1 = []
for i0 in range(len(y1)):
if y0[i0]==-1 and y1[i0]==-1:
re1.append(1/2.0)
else:
re1.append(0)
re1 = np.array(re1)
# print(len(x1))
# print(len(re1))
plt.scatter(x1, re1, s = 30, color = 'orange', label = "$q_{xy}$", marker = "o" )
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 40,
}
font3 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 20,
}
plt.xlim(np.min(x1),np.max(x1))
plt.ylim(-1,1)
plt.xlabel("$m_0$",font2)
plt.ylabel("$q_{xy}$",font2)
plt.yticks([-1,-0.5,0.,0.5,1],fontproperties='Times New Roman', size = 40)
plt.xticks([np.min(x1),-2,0,2,4,np.max(x1)],fontproperties='Times New Roman', size = 40)
plt.legend(loc = 'upper left', bbox_to_anchor=(0.0,0.8), shadow = True, prop = font3, markerscale = 1, borderpad = 0.1)
#plt.text(x = 0.6,y = 0.7,s = 'MCM', fontdict=dict(fontsize=20, color='black',family='Times New Roman'))
#plt.text(x = 0.1,y = 0.7,s = 'NSC', fontdict=dict(fontsize=20, color='black',family='Times New Roman'))
# plt.vlines(x = -0.5, ymin = -1.5, ymax = 1.5,lw = 3.0, colors = 'blue', linestyles = '--')
# plt.vlines(x = 1.0, ymin = -1.5, ymax = 1.5,lw = 3.0, colors = 'blue', linestyles = '--')
plt.vlines(x = 2, ymin = -1.5, ymax = 1.5,lw = 3.0, colors = 'blue', linestyles = '--')
plt.vlines(x = -2, ymin = -1.5, ymax = 1.5,lw = 3.0, colors = 'blue', linestyles = '--')
# plt.text(x = 1.5,y = -0.7,s = '$m_0$=1.0', fontdict=dict(fontsize=20, color='blue',family='Times New Roman'))
# plt.text(x = -3,y = -0.7,s = '$m_0$=-0.5', fontdict=dict(fontsize=20, color='blue',family='Times New Roman'))
# plt.text(x = 7,y = -0.7,s = '$m_0$=8.0', fontdict=dict(fontsize=20, color='black',family='Times New Roman'))
# plt.text(x = -2,y = -0.7,s = '$m_0$=0.0', fontdict=dict(fontsize=20, color='black',family='Times New Roman'))
plt.savefig(picname, dpi = 100, bbox_inches = 'tight')
plt.close()
#---------------------------------------------------------
def main():
for i0 in range(1,2):
mirrorval(i0)
qxy(i0)
#---------------------------------------------------------
if __name__=="__main__":
main()
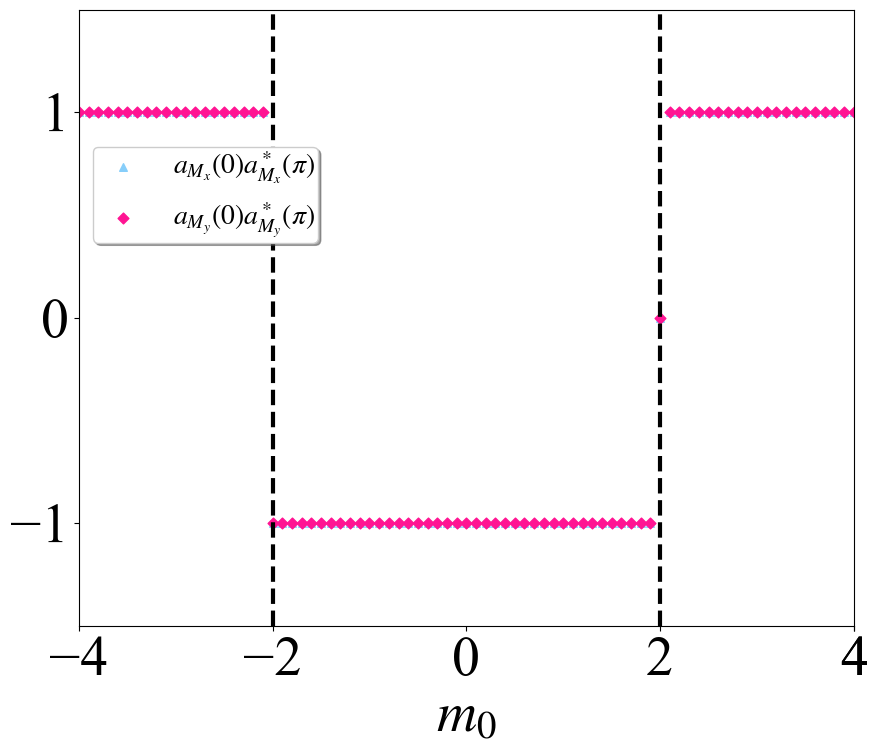
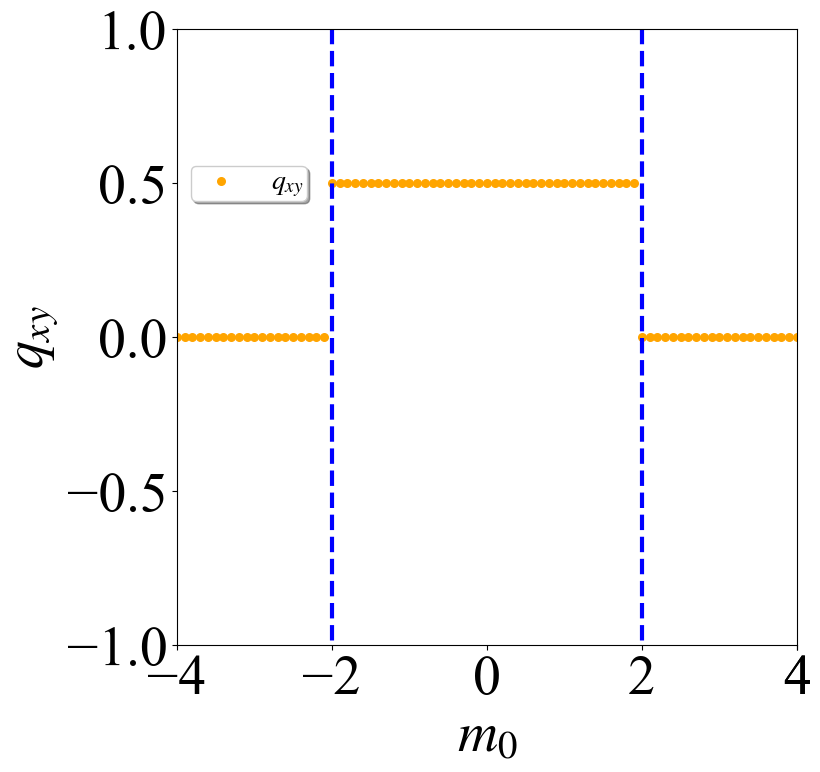
通过上面的计算可以看到,在$m_0\in(-2,2)$的区间内,$\mathcal{M}_x$和$\mathcal{M}_y$的本征值在$0$和$\pi$位置处都是相反的,那么根据
\[\begin{align} \text{exp}\left\{i2\pi p^{\nu^\pm_x}_y\right\} = \alpha^{\pm}_{M_y}(k_x,0) \alpha^{\pm\ast}_{M_y}(k_x,\pi), \end{align}\]就可以确定对应的Wannier sector极化,然后通过两个不同方向的Wannier sector得到体系的电四极矩,计算结果与我们对正常态的分析是符合的。完整的代码和计算结果可以点击这里下载
参数
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |