在之前的博客Julia的MPI并行计算极化率(重复Bilayer Two-Orbital Model of La$_3$Ni$_2$O$_7$ under Pressure)利用Julia计算了一个模型的极化率,但是在撒点数量增加的时候计算速度还是堪忧。这里就返祖利用Fortran语言再结合MPI并行来重写code。根据测试发现计算速度显著提升。
前言
虽然使用Julia在计算的时候速度已经相当快了,但是如果涉及到计算极化率这种需要在布里渊区撒点很多才能精确计算的量,Julia在计算的时候需要的时间还是有点久。况且想要速度更快,就需要仔细的去对代码进行优化,想想还是挺复杂的。最后考虑直接返祖,就用Fortran(公式翻译器)来计算极化率。
关于公式具体的内容可以参考Julia的MPI并行计算极化率(重复Bilayer Two-Orbital Model of La$_3$Ni$_2$O$_7$ under Pressure)这篇Blog,或者去查看原文Bilayer Two-Orbital Model of La$_3$Ni$_2$O$_7$ under Pressure,下面直接上代码。
代码
这里在写的时候偷懒了,将哈密顿量设置为全局变量了,而且对角化厄米矩阵的函数并没有进行封装,调用之后就是直接对角化哈密顿量。实际上正确且安全的写法就是通过子过程返回哈密顿量,并将其传递给对角化函数计算本征值和本征矢量,这样才能让程序具有通用性。不过事情我是知道的,但这个程序很简单,就先不做这样做了,后续写大程序的时候就会规范了。
- 计算耗时
这里撒点数量为 256 * 256,调用了64个核,计算时间如下
======== Job starts at 2024-04-15 15:25:16 on n26 ======== Start Fortran code ======== Job ends at 2024-04-15 15:25:37 on n26 ========下面就是完整的代码了
module param implicit none integer kn,hn parameter(kn = 64,hn = 4) real,parameter::pi = 3.1415926535897 real,parameter::omega = 0.00 complex,parameter::im = (0.,1.) !Imagine unit complex Ham(hn,hn),Umat(hn,hn),ones(hn,hn) ! Hamiltonian and interaction Matrix real t0,t1x,t1z,t2x,t2z,t3xz,t4xz,tvx,tvz,ex,ez ! 哈密顿量参数 real U0,J0 ! 相互作用参数 real valmesh(2,-kn:kn-1,-kn:kn-1,hn) complex vecmesh(2,-kn:kn-1,-kn:kn-1,hn,hn) complex chi0(-kn:kn-1,-kn:kn-1,hn,hn),chi(-kn:kn-1,-kn:kn-1,hn,hn) ! LAPACK PACKAGE PARAM integer::lda = hn integer,parameter::lwmax = 2*hn+hn**2 real,allocatable::val(:) complex,allocatable::work(:) real,allocatable::rwork(:) integer,allocatable::iwork(:) integer lwork ! at least 2*hn+N**2 integer lrwork ! at least 1 + 5*hn +2*hn**2 integer liwork ! at least 3 +5*hn integer info end module param !================================================================================================================================================================================================ program main use param use mpi !------------------------------------ complex temp1(hn,hn),temp2(hn,hn),temp3 integer iky,ikx real qx,qy,local_rechi(-kn:kn-1,-kn:kn-1,4),rechi(-kn:kn-1,-kn:kn-1,4) !--------------------------------- integer numcore,indcore,ierr character(len=20)::filename,char1,char2 !--------------------------------- external::cheevd allocate(val(hn)) allocate(work(lwmax)) allocate(rwork(1+5*hn+2*hn**2)) allocate(iwork(3+5*hn)) !--------------------------------- call MPI_INIT(ierr) ! 初始化进程 call MPI_COMM_RANK(MPI_COMM_WORLD, indcore, ierr) ! 得到本进程在通信空间中的rank值,即在组中的逻辑编号(该 rank值为0到p-1间的整数,相当于进程的ID。) call MPI_COMM_SIZE(MPI_COMM_WORLD, numcore, ierr) !获得进程个数 size, 这里用变量p保存 call MPI_Barrier(MPI_COMM_WORLD,ierr) nki = floor(indcore * (2.0 * kn)/numcore) - kn nkf = floor((indcore + 1) * (2.0 * kn)/numcore) - kn - 1 ! 遍历BZ求极化率 do iky = nki,nkf qy = pi * iky/kn do ikx = -kn,kn - 1 qx = pi * ikx/kn call chi0cal(qx,qy,chi0(iky,ikx,:,:)) ! 得到裸极化率 call inv(ones - matmul(chi0(iky,ikx,:,:),Umat),temp2) ! 矩阵求逆 chi(iky,ikx,:,:) = matmul(temp2,chi0(iky,ikx,:,:)) temp3 = sum(chi(iky,ikx,:,:)) local_rechi(iky,ikx,1) = qx local_rechi(iky,ikx,2) = qy local_rechi(iky,ikx,3) = real(temp3) local_rechi(iky,ikx,4) = aimag(temp3) end do end do call MPI_Barrier(MPI_COMM_WORLD,ierr) ! call MPI_Gather(local_rechi, 2 * kn, MPI_COMPLEX, rechi, 2 * kn, MPI_COMPLEX, 0, MPI_COMM_WORLD,ierr) call MPI_Reduce(local_rechi, rechi, (2 * kn)**2 * 4, MPI_REAL, MPI_SUM, 0, MPI_COMM_WORLD,ierr) if (indcore .eq. 0) then char1 = "fortran-chi-" write(char2,"(I3.3)")kn filename = trim(char1)//trim(char2) char1 = ".dat" filename = trim(filename)//trim(char1) open(12,file = filename) do iky = -kn,kn - 1 do ikx = -kn,kn - 1 write(12,"(4F5.3)")rechi(iky,ikx,1),rechi(iky,ikx,2),abs(rechi(iky,ikx,3)),abs(rechi(iky,ikx,4)) end do end do close(12) end if call MPI_Finalize(ierr) stop end program main !================================================================================================================================================================================================ subroutine matset(kx,ky) ! 矩阵赋值 use param real kx,ky integer k0 t0 = 1.0 t1x = -0.483 * t0 t1z = -0.110 * t0 t2x = 0.069 * t0 t2z = -0.017 * t0 t3xz = 0.239 * t0 t4xz = -0.034 * t0 tvx = 0.005 * t0 tvz = -0.635 * t0 ex = 0.776 * t0 ez = 0.409 * t0 Ham = 0.0 Ham(1, 1) = 2 * t1x * (cos(kx) + cos(ky)) + 4 * t2x * cos(kx) * cos(ky) + ex Ham(2, 2) = 2 * t1z * (cos(kx) + cos(ky)) + 4 * t2z * cos(kx) * cos(ky) + ez Ham(1, 2) = 2 * t3xz * (cos(kx) - cos(ky)) Ham(2, 1) = 2 * t3xz * (cos(kx) - cos(ky)) Ham(3, 3) = 2 * t1x * (cos(kx) + cos(ky)) + 4 * t2x * cos(kx) * cos(ky) + ex Ham(4, 4) = 2 * t1z * (cos(kx) + cos(ky)) + 4 * t2z * cos(kx) * cos(ky) + ez Ham(3, 4) = 2 * t3xz * (cos(kx) - cos(ky)) Ham(4, 3) = 2 * t3xz * (cos(kx) - cos(ky)) Ham(1, 3) = tvx Ham(1, 4) = 2 * t4xz * (cos(kx) - cos(ky)) Ham(2, 3) = 2 * t4xz * (cos(kx) - cos(ky)) Ham(2, 4) = tvz Ham(3, 1) = tvx Ham(4, 1) = 2 * t4xz * (cos(kx) - cos(ky)) Ham(3, 2) = 2 * t4xz * (cos(kx) - cos(ky)) Ham(4, 2) = tvz !--------------------------------------------------------------------- ! 相互作用矩阵赋值 U0 = 3.0 J0 = 0.4 Umat(1,1) = U0 Umat(2,2) = U0 Umat(3,3) = U0 Umat(4,4) = U0 Umat(1,2) = J0/2 Umat(2,1) = J0/2 Umat(3,4) = J0/2 Umat(4,3) = J0/2 !--------------------------------------------------------------------- ! 单位矩阵 do k0 = 1,hn ones(k0,k0) = 1 end do return end subroutine !================================================================================================================================================================================================ subroutine chi0cal(qx,qy,re1) ! 计算极化率 返回到re1 use param integer ikx,iky,l1,l2,e1,e2 real qx,qy,kx,ky complex re1(hn,hn) do iky = -kn,kn - 1 ky = pi * iky/kn do ikx = -kn,kn - 1 kx = pi * ikx/kn ! k call matset(kx,ky) call eigSol() valmesh(1,iky,ikx,:) = val(:) vecmesh(1,iky,ikx,:,:) = Ham(:,:) ! k + q call matset(kx + qx,ky + qy) call eigSol() valmesh(2,iky,ikx,:) = val(:) vecmesh(2,iky,ikx,:,:) = Ham(:,:) ! 计算极化率 do l1 = 1,hn ! orbit ondex do l2 = 1,hn do e1 = 1,hn ! band index do e2 = 1,hn re1(l1,l2) = re1(l1,l2) + (fermi(valmesh(1,iky,ikx,e1)) - fermi(valmesh(2,iky,ikx,e2)))/(im * (omega + 0.0001) + valmesh(1,iky,ikx,e1) - valmesh(2,iky,ikx,e2))& * conjg(vecmesh(2,iky,ikx,l1,e2)) * vecmesh(2,iky,ikx,l2,e2) * conjg(vecmesh(1,iky,ikx,l2,e1)) * vecmesh(1,iky,ikx,l1,e1) end do end do end do end do end do end do re1 = re1/(2 * kn)**2 return end subroutine !================================================================================================================================================================================================ function fermi(ek) ! 费米分布函数 implicit none real fermi,ek,kbt kbt = 0.001 fermi = 1/(exp(ek/kbt) + 1) return end !================================================================================================================================================================================================ function equivkpq(i0) ! 找到BZ中k+q等价与k的索引 use param integer equivkpq,i0 if (i0 <= kn/2 .and. i0 > -kn/2) equivkpq = i0 if (i0 > kn/2) equivkpq = i0 - kn if (i0 <= -kn/2) equivkpq = i0 + kn end !================================================================================================================================================================================================ subroutine eigSol() ! 对角化得到本征值w和本征矢量Ham use param integer m lwork = -1 liwork = -1 lrwork = -1 call cheevd('V','U',hn,Ham,lda,val,work,lwork,rwork,lrwork,iwork,liwork,info) lwork = min(2 * hn + hn**2, int( work( 1 ) ) ) lrwork = min(1 + 5 * hn + 2 * hn**2, int( rwork( 1 ) ) ) liwork = min(3 + 5 * hn, iwork( 1 ) ) call cheevd('V','U',hn,Ham,lda,val,work,lwork,rwork,lrwork,iwork,liwork,info) if( info .GT. 0 ) then open(11,file = "mes.dat",status = "unknown") write(11,*)'The algorithm failed to compute eigenvalues.' close(11) end if ! open(12,file="eigval.dat",status="uknnown") ! do m = 1,N ! write(12,*)m,val(m) ! end do ! close(12) return end subroutine eigSol !================================================================================================================================================================================================ subroutine inv(matin,matout) ! 矩阵求逆 use param complex,intent(in) :: matin(hn,hn) complex:: matout(size(matin,1),size(matin,2)) real:: work2(size(matin,1)) ! work2 array for LAPACK integer::ipiv(size(matin,1)) ! pivot indices ! Store matin in matout to prevent it from being overwritten by LAPACK matout = matin ! SGETRF computes an LU factorization of a general M - by - N matrix A ! using partial pivoting with row interchanges . call CGETRF(hn,hn,matout,hn,ipiv,info) if (info.ne.0) stop 'Matrix is numerically singular!' ! SGETRI computes the inverse of a matrix using the LU factorization ! computed by SGETRF. call CGETRI(hn,matout,hn,ipiv,work2,hn,info) if (info.ne.0) stop 'Matrix inversion failed!' return end subroutine inv !================================================================================================================================================================================================计算结果
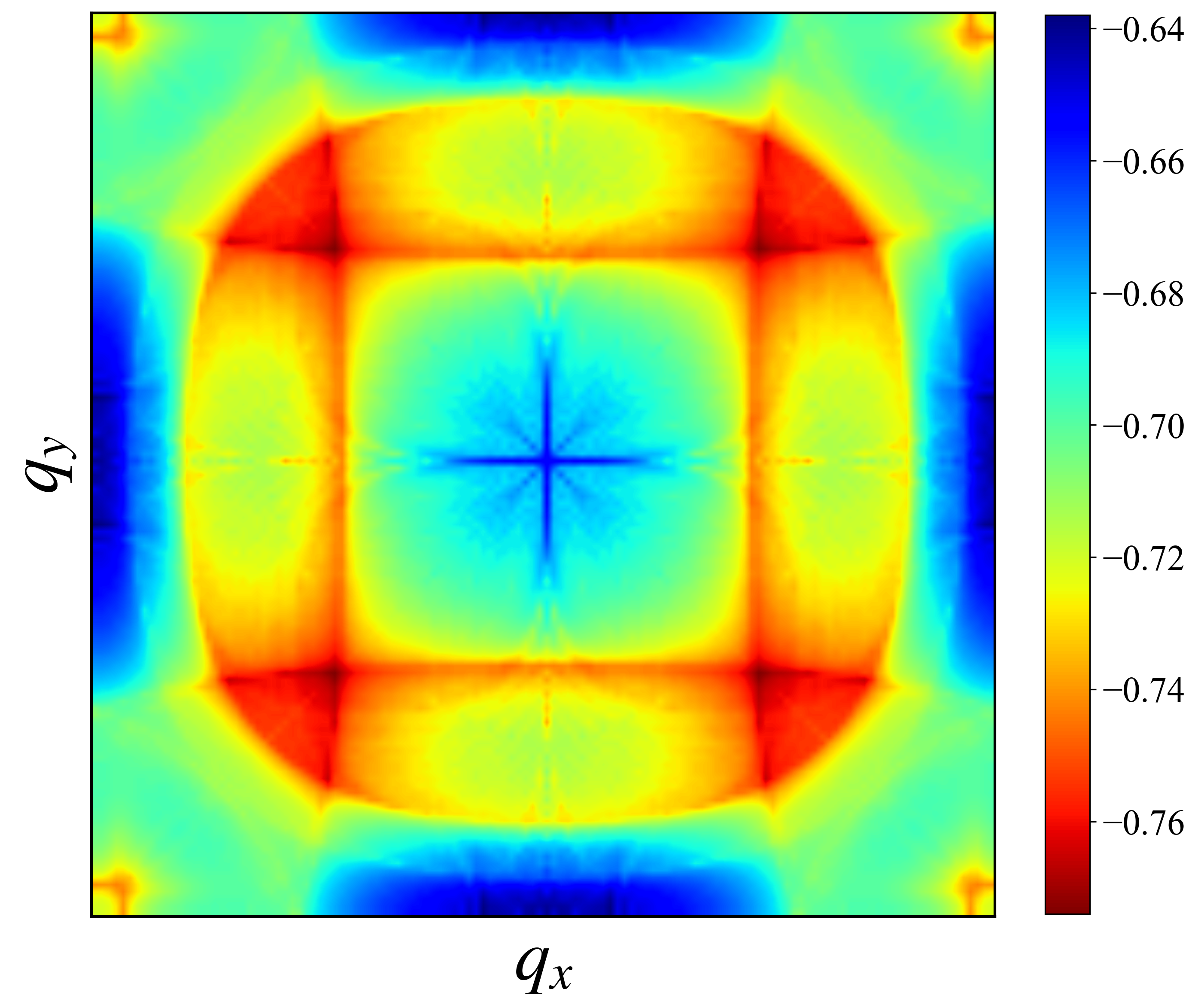
绘图程序
def plotchi(numk):
dataname = "chi-nk-" + str(format(numk,".2f")) + ".dat"
dataname = "julia-chi-nk-" + str(format(numk,".2f")) + ".dat"
dataname = "fortran-chi-" + str(format(numk,"0>3d")) + ".dat" # 补足整数
picname = os.path.splitext(dataname)[0] + ".png"
da = np.loadtxt(dataname)
x0 = da[:,0]
z0 = np.array(da[:,2])
xn = int(np.sqrt(len(x0)))
z0 = z0.reshape(xn,xn)
plt.figure(figsize = (10,10))
# sc = plt.imshow(z0,interpolation='bilinear', cmap = cm.RdYlGn,origin='lower',vmax = abs(z0).max(), vmin = 0)
# sc = plt.imshow(z0,interpolation='bilinear', cmap = "jet",origin='lower', extent=[1, 30, 1, 30],vmax = abs(z0).max(), vmin = 0)
sc = plt.imshow(z0,interpolation='bilinear', cmap = "jet_r",origin='lower')
cb = plt.colorbar(sc,fraction = 0.045) # 调整colorbar的大小和图之间的间距
cb.ax.tick_params(labelsize=20)
font2 = {'family': 'Times New Roman','weight': 'normal','size': 40}
# cb.set_label('ldos',fontdict=font2) #设置colorbar的标签字体及其大小
# plt.scatter(x0, y0, s = 5, color='blue',edgecolor="blue")
plt.axis('scaled')
plt.xlabel(r"$q_x$",font2)
plt.ylabel(r"$q_y$",font2)
# tit = "$J_x= " + str(cont) + "$"
# plt.title(tit,font2)
plt.yticks([],fontproperties='Times New Roman', size = 40)
plt.xticks([],fontproperties='Times New Roman', size = 40)
# plt.tick_params(axis='x',width = 2,length = 10)
# plt.tick_params(axis='y',width = 2,length = 10)
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
# plt.show()
plt.savefig(picname, dpi = 300,bbox_inches = 'tight')
plt.close()
#------------------------------------------------------------
if __name__=="__main__":
plotchi(128)
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |