在正方晶格超导序参量自洽的文章中是利用了自洽方程得到超导序参量，并研究了其温度依赖关系。这里给出利用最小化自由能的方式来得到序参量，并给出金兹堡-朗道(Ginzburg–Landau )理论所给出的自由能随温度的演化。

公式推导

起手先是一个有吸引相互作用的哈密顿量

\[H=\sum_{\mathbf{k},\mathbf{k}^\prime}c^\dagger_{\mathbf{k},s}h(\mathbf{k})_{ss^\prime}c_{\mathbf{k},s^\prime}-U\sum_{\mathbf{k},\mathbf{k}^\prime}c^\dagger_{\mathbf{k}\uparrow}c^\dagger_{-\mathbf{k}\downarrow}c_{-\mathbf{k}^\prime\downarrow}c_{\mathbf{k}^\prime\uparrow}\]

平均场处理之后分解到超导通道，则可以得到BdG哈密顿量，不熟悉可以参考正常态到BdG哈密顿量的构建这篇笔记，或者参考李正中固体理论。超导序参量则需要自洽

\[\Delta=-U\sum_{\mathbf{k}}\langle c_{\mathbf{k}\downarrow}c_{-\mathbf{k}\uparrow}\rangle\]

体系的自由能为

\[F_s=\frac{|\Delta|^2}{U}-\sum_{\mathbf{k},n}\frac{1}{2\beta}\ln(1+e^{-\beta E_n(\mathbf{k})})\]

这里的$E_n(\mathbf{k})$就是BdG哈密顿量的本征值，BdG哈密顿量为

\[H_{\rm BdG}(\mathbf{k})=\left( \begin{array}{cc} h(\mathbf{k})&-i\Delta\sigma_y\\ i\Delta\sigma_y&-h^*(-\mathbf{k}) \end{array} \right)\]

通过给定不同的$\Delta$来对角化$H_{\rm BdG}(\mathbf{k})$得到本征值，从而可以计算自由能，而最小的自由能对应的$\Delta$就是自洽得到的超导序参量，所以这里实际上是通过一种遍历的方式来得到超导序参量的。

结果展示

改变温度，自由能随序参量变化
最大序参量随温度的变化
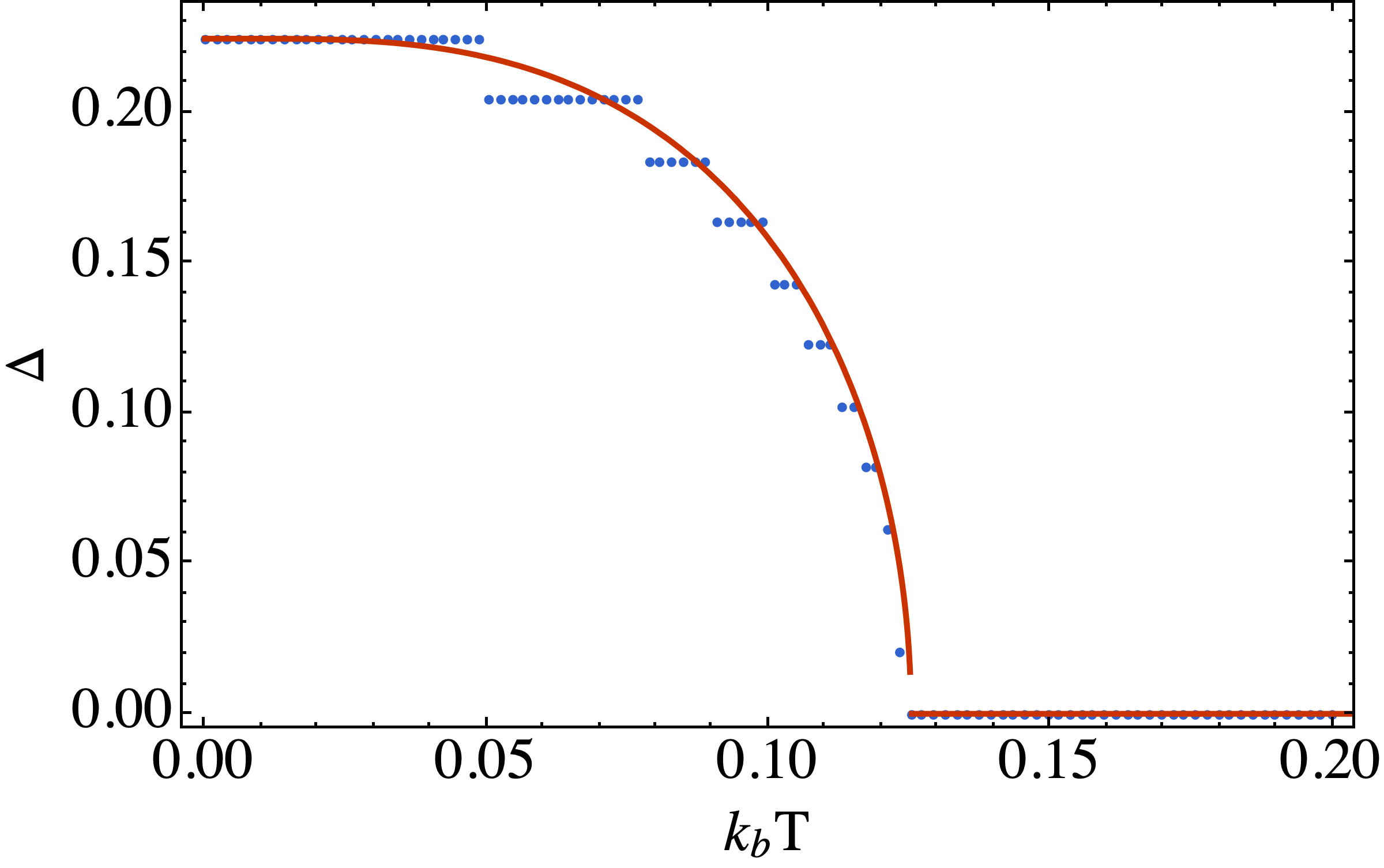
序参量随磁场的变化

png

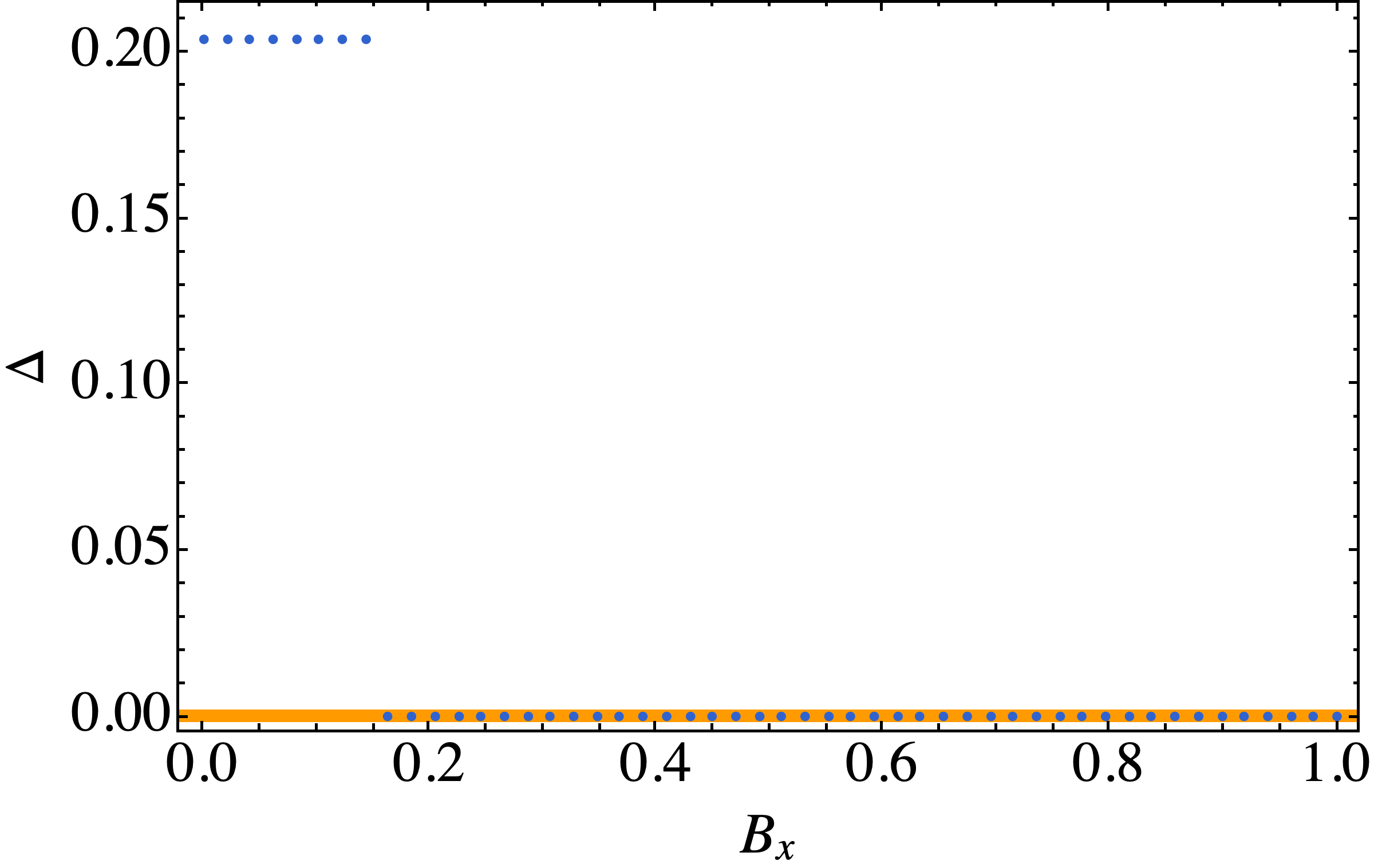
可以发现随着增加磁场，序参量会发生突变，因为这里考虑的模型是自由电子气，Type-I类型的超导体，其超导正常态转变是个二级相变。

根据$\Delta(T = 0)=\Delta_0$时的序参量大小可以近似估计$^{[1]}$破坏超导态的最大临界磁场，在普通的超导体中成为Pauli极限，即外加的磁场使得两种不同的自旋感受到能量差，临界磁场近似为

\[B_c=\frac{\Delta_0}{\sqrt{2}}\]

改变磁场，自由能随序参量的变化

png

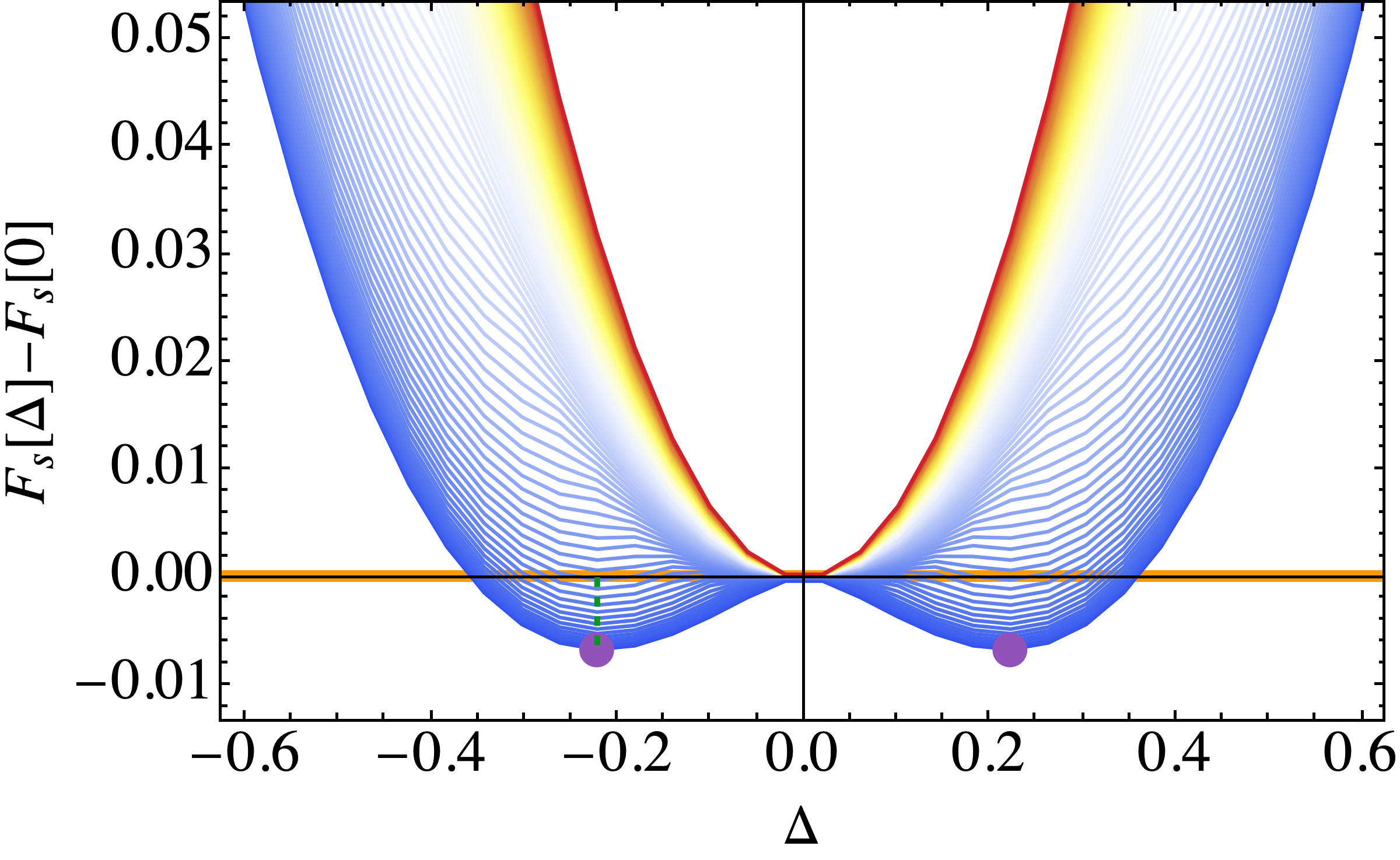
临界磁场与温度之间的依赖关系

png

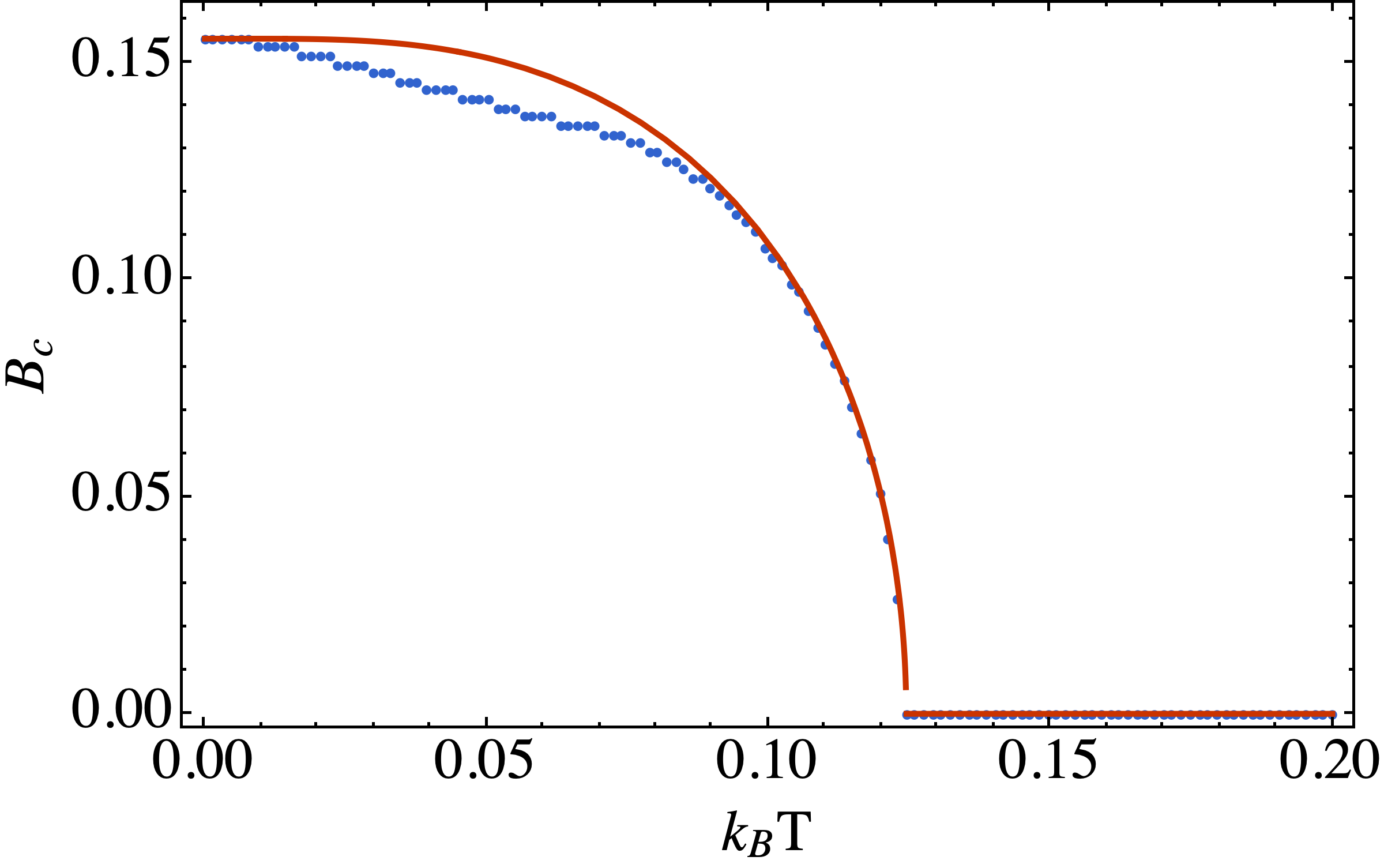
临界磁场($B_c$)与临界温度$Tc$之间的依赖关系,颜色深浅表示该参数下最小自由能对应的超导序参量$\Delta$

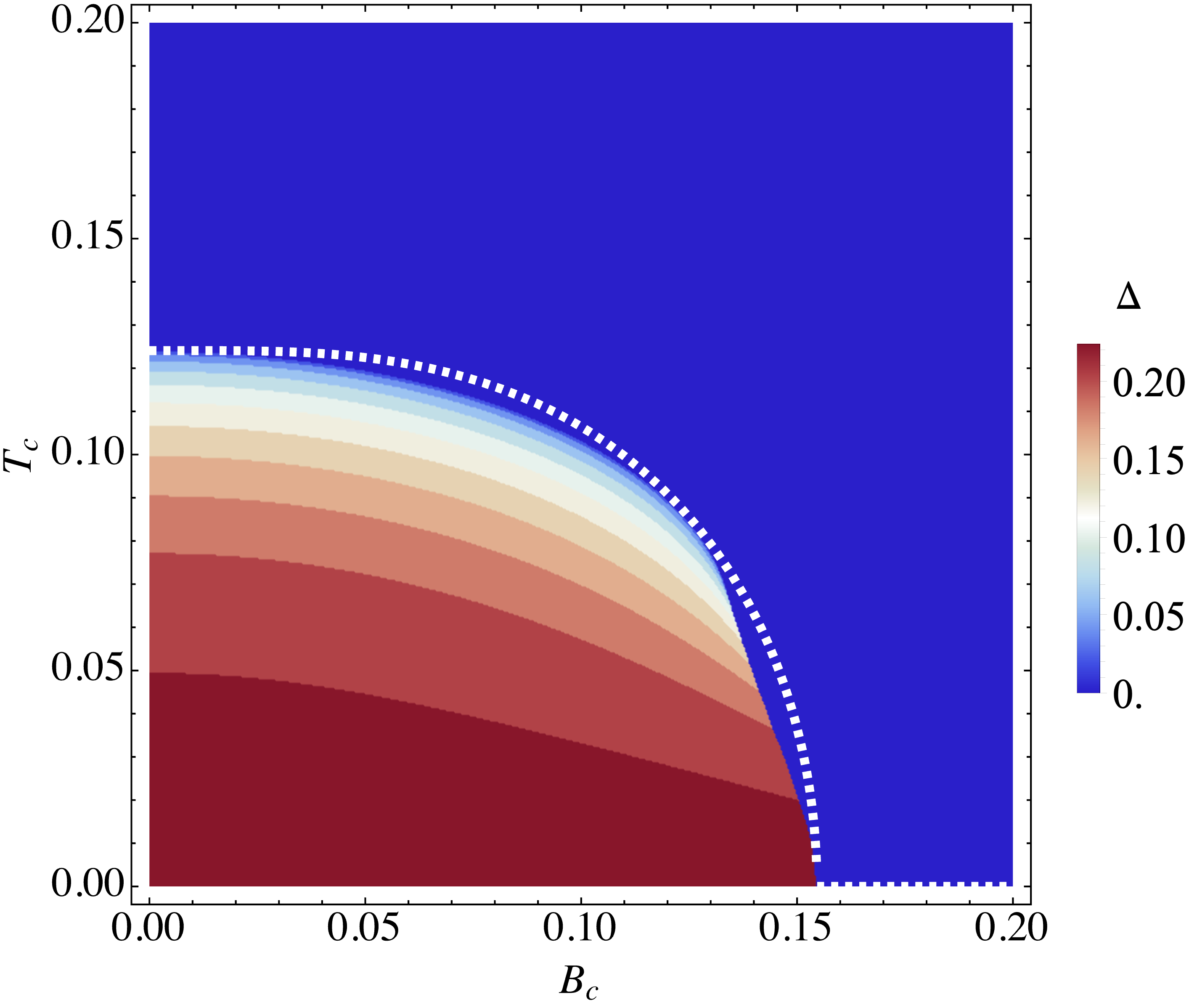
通过公式 $\Delta(T)=\Delta_0\tanh(k \sqrt{\frac{T_c-T}{T}})$ 不仅可以拟合序参量，也可以拟合磁场随温度的改变

数据都打包放在了一起，可以点击这里下载

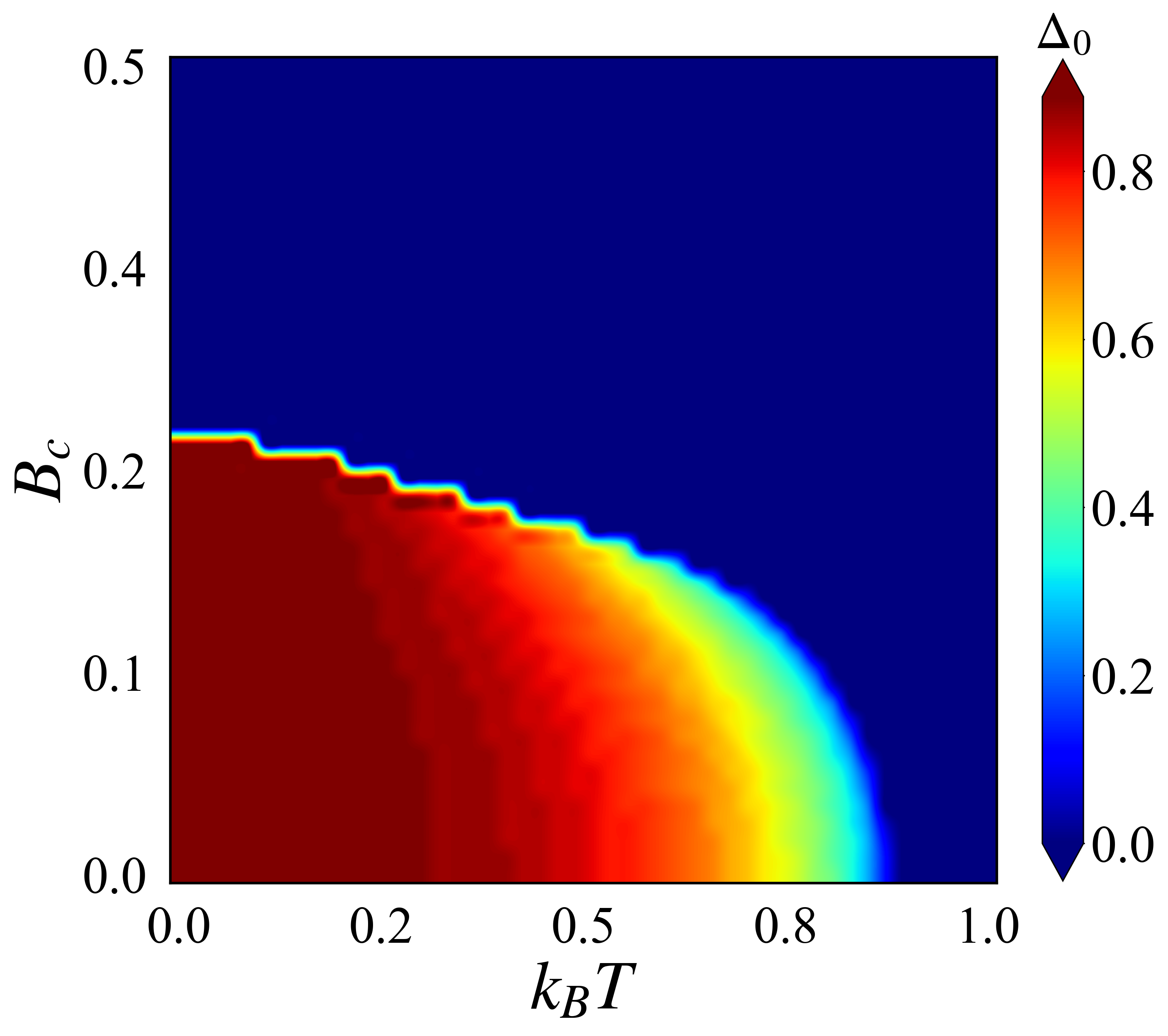
发现用Mathematica绘制的最后一个图效果不是很好，选择用Python重新绘制一下

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
import matplotlib.ticker as mticker
import matplotlib.colors as colors
plt.rc('font', family='Times New Roman')
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#------------------------------------------------------------
def Plot_phase_diagram(numk):
    dataname = "chi-val-kn-" + str(format(numk,"0>3d")) + ".dat"
    dataname = "Bx_kbt-phase.dat"
    picname = os.path.splitext(dataname)[0] + ".png"
    da = np.loadtxt(dataname) 
    # 提取数据
    x0 = np.array(da[0, :])  # x 坐标
    y0 = np.array(da[1, :])  # y 坐标
    z0 = np.array(da[2, :])  # z 值（密度值）
    xn = int(np.sqrt(len(x0)))
    x0 = x0.reshape(xn, xn)
    y0 = y0.reshape(xn, xn)
    z0 = z0.reshape(xn,xn)
    # 确定 x 和 y 的范围
    x_min, x_max = np.min(x0), np.max(x0)
    y_min, y_max = np.min(y0), np.max(y0)

    # 设置图形大小
    plt.figure(figsize=(10, 10))
    # sc = plt.imshow(z0, extent=[x_min, x_max, y_min, y_max],  interpolation = 'spline16', cmap = "jet",  origin = 'lower',aspect='auto')  
    sc = plt.imshow(z0,   interpolation = 'spline16', cmap = "jet",  origin = 'lower')  
    # 标记密度为 0 的边界
    # zero_contour = plt.contour(x0, y0, z0, levels = [0.00078431], colors='black', linewidths=2)  
    # plt.clabel(zero_contour, inline=True, fontsize=10, fmt='0')
    cb = plt.colorbar(sc,fraction = 0.045,extend='both')  # 调整colorbar的大小和图之间的间距
    # cb.ax.tick_params(labelsize = 20)
    cb.ax.tick_params(size = 0.8)
    cb.ax.set_title(r"$\Delta_0$", fontsize = 30)
    font2 = {'family': 'Times New Roman','weight': 'normal','size': 40}
    # # cb.set_label('ldos',fontdict=font2) #设置colorbar的标签字体及其大小
    # # plt.scatter(x0, y0, s = 5, color='blue',edgecolor="blue")
    plt.axis('scaled')
    # plt.gca().set_aspect('equal')
    plt.xlabel(r"$k_BT$",font2)
    plt.ylabel(r"$B_c$",font2)
    # tit = "$J_x= " + str(cont) + "$"
    # plt.title(tit,font2)
    # 设置刻度标签
    # 设置横纵坐标刻度
    xticks = np.linspace(0, z0.shape[1] - 1, num = 5)  # 将横坐标分为 5 个刻度
    yticks = np.linspace(0, z0.shape[0] - 1, num = 5)  # 将纵坐标分为 5 个刻度
    xtick_labels = np.linspace(x_min, x_max, num = 5)  # 横坐标标签
    ytick_labels = np.linspace(y_min, y_max, num = 5)  # 纵坐标标签
    plt.xticks(xticks, labels=[f"{x:.1f}" for x in xtick_labels])  # 设置横坐标刻度和标签
    plt.yticks(yticks, labels=[f"{y:.1f}" for y in ytick_labels])  # 设置纵坐标刻度和标签
    plt.tight_layout()
    # plt.yticks([],fontproperties='Times New Roman', size = 40)
    # plt.xticks([],fontproperties='Times New Roman', size = 40)
    plt.tick_params(axis='x',width = 0.,length = 10)
    plt.tick_params(axis='y',width = 0,length = 10)
    ax = plt.gca()
    ax.locator_params(axis='x', nbins = 5)  # x 轴最多显示 3 个刻度
    ax.locator_params(axis='y', nbins = 5)  # y 轴最多显示 3 个刻度
    ax.spines["bottom"].set_linewidth(1.5)
    ax.spines["left"].set_linewidth(1.5) 
    ax.spines["right"].set_linewidth(1.5)
    ax.spines["top"].set_linewidth(1.5)
    # plt.show()
    plt.savefig(picname, dpi = 300,bbox_inches = 'tight')
    plt.close()
#------------------------------------------------------------
if __name__=="__main__":
    # plotband()
    kn = 128
    Plot_phase_diagram(kn)