空间群操作对Bloch函数的影响以及空间群的表示
空间群操作对Bloch函数的作用
对一个空间群操作
\[\{S\rvert\mathbf{w}\}\psi(\mathbf{r}=\psi(S^{-1}(\mathbf{r-w}))\]首先可以证明
\[\exp(i\mathbf{k}\cdot S\mathbf{r})=\exp(iS^{-1}\mathbf{k}\cdot\mathbf{r})\]这是因为
\[\mathbf{k}\cdot S\mathbf{r}=\sum_{ij}k_iS_{ij}r_j=\sum_{ij}S^T_{ji}k_ir_j=\sum_{ij}S^{-1}_{ji}k_ir_j\]因为$S$是点群操作,其表示是个正交矩阵满足$S^T=S^{-1}$,即可以得到
\[\{S\rvert\mathbf{w}\}\exp(i\mathbf{k}\cdot\mathbf{r})=\exp(i\mathbf{k}\cdot S^{-1}(\mathbf{r-w}))=\exp(iS\mathbf{k}\cdot(\mathbf{r-w}))\]这也就将本来作用在实空间中的点群操作$S$变换到了作用在倒空间$\mathbf{k}$上,此时相当于是一个中心在$\mathbf{r=w}$处,波矢为$S\mathbf{k}$的一个函数.
同样的可以定义
\[u_{S\mathbf{k}}(\mathbf{r-w})=u_\mathbf{k}\{S^{-1}(\mathbf{r-w})\}=\{S\rvert\mathbf{w}\}u_\mathbf{k}(\mathbf{r})\]这里的$u_\mathbf{k}(\mathbf{r})$是元胞的波函数,满足和其相同的对称性$u_\mathbf{k}(\mathbf{r})=u_\mathbf{k}(\mathbf{r+t})$,结合上面的性质就可以定义出Bloch函数
\[\Psi_\mathbf{k}(\mathbf{r})=\exp(i\mathbf{k}\cdot\mathbf{r})u_\mathbf{k}(\mathbf{r})\]从而可以得到
\[\{S\rvert\mathbf{w}\}\psi_\mathbf{k}(\mathbf{r})=\exp(iS\mathbf{k}\cdot(\mathbf{r-w}))u_{S\mathbf{k}}(\mathbf{r-w})=\psi_{S\mathbf{k}}(\mathbf{r-w})\]将空间群操作作用在Bloch波函数上,不仅实空间位置$\mathbf{r}$要发生改变,对应的$\mathbf{k}$也会受到点群操作$S$的影响.同样也可以得到
\[\{S\rvert\mathbf{w}\}\{R\rvert\mathbf{v}\}\psi_\mathbf{k}(\mathbf{r})=\psi_{SR\mathbf{k}}(\mathbf{r-w}-S\mathbf{v})\]因为$u_{S\mathbf{k}}$还满足$u_\mathbf{k}(\mathbf{r})=u_\mathbf{k}(\mathbf{r+t})$,如果$\mathbf{t}$是平移那么$\mathbf{t}^{‘}=S^{-1}\mathbf{t}$,因此
\[u_{S\mathbf{k}}(\mathbf{r-w+t})=u_\mathbf{k}(S^{-1}(\mathbf{r-w+t}))=u_\mathbf{k}(S^{-1}(\mathbf{r-w})+\mathbf{t}^{'})=u_\mathbf{k}(S^{-1}(\mathbf{r-w}))=u_{S\mathbf{k}}(\mathbf{r-w})\]空间群操作${S\rvert\mathbf{w}}$作用在中心为$\mathbf{r}=0$波矢为$\mathbf{k}$的Bloch函数上会将其变换为波矢为$S\mathbf{k}$中心在$\mathbf{r=w}$处的一个Bloch波函数.
从前面可以看到,空间群操作作用在平面波和Bloch函数上具有一定的相似性,但是这里有一个很重要的不同点,当$S\mathbf{k}=\mathbf{k}$的时候(相等关系),也就是说点群操作将一个波矢$\mathbf{k}$变换到其本身,
\[\{S\rvert\mathbf{w}\}\psi_\mathbf{k}(\mathbf{r})=\exp(i\mathbf{k}\cdot(\mathbf{r-w}))\]此时平面波的中心在$\mathbf{r=w}$处.如果$S\mathbf{k}\equiv\mathbf{k}$(等价关系)却并不要求${S\rvert\mathbf{w}}\psi_\mathbf{k}(\mathbf{r})=\psi_\mathbf{k}(\mathbf{r-w})$,这是因为波函数$\psi_\mathbf{k}$上的标记$\mathbf{k}$此时代表的仅仅是等价关系.
在$\mathbf{k}=0$处$S\mathbf{k}=\mathbf{k}$是平庸的结果,零$\psi_0(\mathbf{r})=1+\exp(i\mathbf{g}\cdot\mathbf{r})$那么存在
\[\{S\rvert\mathbf{w}\}\psi_0(\mathbf{r})=\psi_0(S^{-1}\mathbf{r}-S^{-1}\mathbf{w})=1+\exp(i\mathbf{g}\cdot S^{-1}(\mathbf{r-w}))=1+\exp(iS\mathbf{g}\cdot(\mathbf{r-w}))\]如果要令上式右端等于$\psi_0$那么就会要求$S\mathbf{g}=\mathbf{g}$,只有当$S\mathbf{g}$和$\mathbf{g}$等价的时候才是成立的,此时相对应的波矢$\mathbf{k}=0$.
定理:如果$\psi_\mathbf{k}(\mathbf{r})$是波矢为$\mathbf{k}$的Bloch波函数,那么${E\rvert\mathbf{t}}\psi_\mathbf{k}(\mathbf{r})=\exp(i\mathbf{k}\cdot\mathbf{t})\psi_\mathbf{k}(\mathbf{r})$,那么${S\rvert\mathbf{w}}\psi_\mathbf{k}(\mathbf{r})$是波矢为$S\mathbf{k}$的Bloch函数.
下面来证明上面的定理,将平移操作作用到上面的Bloch函数上
\[\begin{equation}\begin{aligned}\{E\rvert\mathbf{t}\}\{S\rvert\mathbf{w}\}\psi_\mathbf{k}(\mathbf{r})&=\{S\rvert\mathbf{w}\}\psi_\mathbf{k}(\mathbf{r-t})\\&=\psi_\mathbf{k}(S^{-1}(\mathbf{r-t-w}))=\psi_{S\mathbf{k}}(\mathbf{r-t-w})\\&=\{E\rvert\mathbf{t}\}\psi_{S\mathbf{k}}(\mathbf{r-w})=\exp(-iS\mathbf{k}\cdot\mathbf{t})\psi_{S\mathbf{k}}(\mathbf{r-w})\\&=\exp(-iS\mathbf{k}\cdot\mathbf{t})\{S\rvert\mathbf{w}\}\psi_\mathbf{k}(\mathbf{r})\end{aligned}\end{equation}\]这里同样可以有一个推论,如果$S\mathbf{k}\equiv\mathbf{k}$,那么${S\rvert\mathbf{w}}\psi_\mathbf{k}(\mathbf{r})$是波矢为$\mathbf{k}$的Bolch函数.
空间群表示理论
对一个空间群$\mathbf{G}$,它的平移操作部分$\mathbf{T}$是其子群,其对应的表示$\Delta^\mathbf{k}$为
\[\Delta^\mathbf{k}(\{E\rvert\mathbf{t}\})=\exp(-i\mathbf{k}\cdot\mathbf{t})\]将空间群根据子群$\mathbf{T}$进行陪集分解
\[\mathbf{G}=\{R_1\rvert\mathbf{v}_1\}\mathbf{T}+\{R_2\rvert\mathbf{v}_2\}\mathbf{T}+\cdots+\{R_h\rvert\mathbf{v}_h\}\mathbf{T}\]这里可以选择$R_1=E,\mathbf{v}_1=0$,其余的$\mathbf{v}_i$都是与$R_i$相互关联.这些陪集表示可以构成一个集合$\mathbf{Q}$,但是并不一定就可以构成一个群.商群$\mathbf{G}/\mathbf{T}$是一个群,它与操作$R_1,R_2,\cdots,R_h$构成的点群$\mathbf{F}$是同构的,且$\mathbf{F}$与空间群$\mathbf{G}$是同形的(isogonal).
表示域(Representation domain):对于任意一个空间群$\mathbf{G}$都存在一个表示域$\Phi$,这个空间群对应的布里渊区而言,$\sum_RR\Phi$就是整个布里渊区的体积,这里的$R$是对群$\mathbf{F}$中所有的元素进行求和. {.:info}
在前面曾介绍过基本区域的概念,这里来比较一下这二者的区别.对一个空间群而言,如果他的同形群$\mathbf{F}$是与这个空间群相关联的晶格系统的全对称群,即$\mathbf{F}=\mathbf{P}$,那么基本区域和表示域是相同的$\Phi=\Omega$.然而通常情况下,$\mathbf{F}$都是$\mathbf{P}$的子群,如果$\rvert\mathbf{P}\rvert/\rvert\mathbf{f}\rvert=i$,那么表示域(Representation domain)的体积$\Phi$就是基本区域(basic domain)$\Omega$的$i$倍.
尽管布里渊区的$\Omega$是确定的,但是表示域的体积$\Phi$将会随着考虑的空间群而发生变化.
Neumann principle:如果一个系统包含确定的对称操作$\mathbf{G}$,那么这个系统的任何物理可观测量也一定具有这些对称操作.
Wigner’s Theorem:如果$R$是哈密顿量$\mathbf{H}$的一个对称操作,$\mathbf{H}$描述一个量子力学系统且$\psi$是它的本征函数,那么$R\psi$同样是$\mathbf{H}$的本征函数,对应着和$\psi$相同的本征值.
将上面的定理进行翻译也就是说,一个粒子的波函数$\psi$就是$\mathbf{G}$的不可约表示的一个基函数.
假设$\Gamma$是群$\mathbf{G}$作用在$d$为空间$V$上的一个表示,加入只考虑$\Gamma$中那些表示平移的元素,那么它们形成的$\mathbf{T}$的表示通常是可约的.
假设可以将其约化到$\mathbf{T}$的不可约表示上,标记为
\[\mathbf{k}_1,\mathbf{k}_1,\cdots,\mathbf{k}_d\]这些表示都是一维的,它们所对应的Bloch波函数为
\[\psi_{\mathbf{k}_1}(\mathbf{r}),\psi_{\mathbf{k}_2}(\mathbf{r}),\cdots,\psi_{\mathbf{k}_d}(\mathbf{r})\]以这些函数为基,平移群$\mathbf{T}$的表示都是对角矩阵,而且这些对角元素$\Gamma({E\rvert\mathbf{t}})$为$\exp(-i\mathbf{k}_p\cdot\mathbf{t})$.
此时矢量
\[\mathbf{k}_1,\mathbf{k}_1,\cdots,\mathbf{k}_d\]并不都是不同的,也就是说在其中存在着等价的矢量满足$S\mathbf{k}\equiv\mathbf{k}$,这里需要的只是所有的不等价的矢量$\mathbf{k}$;事实上,$\mathbf{\Gamma}$是个表示也就意味着如果从$\psi_\mathbf{k}(\mathbf{r})$开始,当空间群$\mathbf{G}$中的任意一个操作元${S\rvert\mathbf{w}}$作用到函数上${S\rvert\mathbf{w}}$那么就可以得到基函数中$d$个Bloch函数的线性组合,也就是说$S\mathbf{k}$是
\[\mathbf{k}_1,\mathbf{k}_1,\cdots,\mathbf{k}_d\]中的一员;线性空间$V$在空间群$\mathbf{G}$的不可约性也就是说,当遍历空间群中的所有元素作用在函数$\psi_\mathbf{k}(\mathbf{r})$上之后,就可以得到整个线性空间.
在群$\mathbf{F}$的某些元素作用下,$\mathbf{k}_1$将会被变换成一系列$\mathbf{k}_1,\mathbf{k}_1,\cdots,\mathbf{k}_d$.
Star:在$\mathbf{k}_i$的集合中,一系列不同的$\mathbf{k}$矢量构成了$\Gamma$的Star,这里两个波矢等价并不是相同的,即$S\mathbf{k}_i=\mathbf{k}_j$,但$\mathbf{k}_i$和$\mathbf{k}_j$仍然是不同的波矢.
在上面的定义中,无论选取的初始矢量是哪一个,在遍历$\mathbf{F}$中的操作之后,都可以得到相同的$\mathbf{k}_i$序列.
小共群(Little co-group):群$\mathbf{F}$中的元素,使得波矢$\mathbf{k}_1$不变,$R\in\mathbf{F},R\mathbf{k}_1\equiv\mathbf{k}_1$,这些操作可以构成群$\mathbf{F}$的一个子群,这个子群叫做$\mathbf{k}_1$的小共群,标记为$\bar{G}^{\mathbf{k}_1}$.(这里的操作变换用到的是等价$\equiv$)
因为$\bar{G}^{\mathbf{k}_1}$是$\mathbf{F}$的子群,那么它的阶数一定是$\mathbf{F}$的阶数的因子(拉格朗日定理).小共群$\bar{G}^{\mathbf{k}_1}$中的操作操作$R$满足$R\mathbf{k}_1\equiv\mathbf{k}_1,S$是个固定操作满足$S\mathbf{k}_1=\mathbf{k}_2$,则可以得到$SRS^{-1}\mathbf{k}_2\equiv SR\mathbf{k}_1\equiv S\mathbf{k}_1\equiv\mathbf{k}_2$,也就是说可以得到
\[SRS^{-1}\mathbf{k}_2\equiv\mathbf{k}_2\]这也就意味着$S\bar{G}^{\mathbf{k}_1}S^{-1}$中的元素都包含在$\bar{G}^{\mathbf{k}_2}$中,说明小共群$\bar{G}^{\mathbf{k}_2}$的阶数必然是大于等于$\bar{G}^{\mathbf{k}_1}$的阶数.但是因为存在$\mathbf{k}_1\equiv S^{-1}\mathbf{k}_2$,所以$S\bar{G}^{\mathbf{k}_2}S^{-1}$中的每个元素又都包括在$\bar{G}^{\mathbf{k}_1}$中,因此一个Star的小共群的阶数都是相同的,而且因为$S\bar{G}^{\mathbf{k}_1}S^{-1}=\bar{G}^{\mathbf{k}_1}$的存在,对其它所有的小共群也都是满足的,从而可以发现一个Star中的元素的小共群之间形成了一系列共轭子群.
下面来确定满足$\mathbf{P}\mathbf{k}_1=\mathbf{k}_2,\mathbf{P}\in\mathbf{F}$的数目.取$T\in\mathbf{F}$是个固定的操作满足$T\mathbf{k}_2\equiv\mathbf{k}_1$,那么$T\mathbf{P}\mathbf{k}_1\equiv T\mathbf{k}_2\equiv\mathbf{k}_1$,因此可以得到$T\mathbf{P}\in\bar{\mathbf{G}}^{\mathbf{k}_1}$,从而可以确定操作$\mathbf{P}$授予左陪集$T^{-1}\bar{\mathbf{G}}^{\mathbf{k}_1}$,从而可以看出满足条件的$\mathbf{P}$的数目和小共群的阶数是相同的.如果将群$\mathbf{F}$根据star的任意一个小共群写成左陪集的直和,那么这些陪集将和star中的元素一一对应,反过来可以得到,这些小共群的阶数的乘积正好就是群$\mathbf{F}$的阶数.
不失一般性的,对于一个波矢$\mathbf{k}_1$,不包括那些由star产生的,它总会处在布里渊区表示域内部或者表面上.
一个表示域在定义的时候总是会包含每个star中至少一个$\mathbf{k}$矢量.
当$\mathbf{k}_1$在基本区域(Basic domain)中,$\bar{\mathbf{G}}^{\mathbf{k}_1}$中的对称点和对称线上的元素可以从Table-3.6中直接获取到,此时每个$\bar{\mathbf{G}}^{\mathbf{k}_1}$中的元素都是$\mathbf{P}(\mathbf{k})$中的元素,同样也是$\mathbf{F}$中的元素,$\mathbf{F}$与空间群$\mathbf{G}$是同形的.
当$\mathbf{k}_1$是表示域(Representation domain)中的一部分而不是在基本区域(Basic domain)中,那么$\bar{\mathbf{G}}^{\mathbf{k}_1}$中的元素与$\bar{\mathbf{G}}^{\mathbf{k}}$中的元素可以简单的联系起来,这里$\mathbf{k}$是在基本区域内,通过全对称点群$\mathbf{P}$中的一个操作$R$可以得到$R\mathbf{k}_1\equiv\mathbf{k}$,那么立即就可以得到
\[\mathbf{P}(\mathbf{k}_1)=R^{-1}\mathbf{P}(\mathbf{k})R\]这里的$\mathbf{P}(\mathbf{k})$可以从Table-3.6中得到,那么$\mathbf{P}(\mathbf{k}_1)$就是其对应的共轭.此时$\bar{G}(\mathbf{k}_1)$是$\mathbf{P}(\mathbf{k}_1)$和$\mathbf{F}$的交集部分.
little group:假设小共群$\bar{\mathbf{G}}^{\mathbf{k}_1}$中包含$b$个元素$S_1,S_2,\cdots,S_b$,寻找空间群$\mathbf{G}$对于平移群$\mathbf{T}$的左陪集,并将这些陪集中旋转部分为$S_1,S_2,\cdots,S_b$的进行理论求和构成一个集合,它是空间群$\mathbf{G}$的子群,被称为$\mathbf{k}_1$的小群,标记为$\mathbf{G}^{\mathbf{k}_1}$.就像$\bar{G}^{\mathbf{k}_1}$不必要是$\mathbf{F}$的不变子群,此时$\mathbf{G}^{\mathbf{k}_1}$也不必要是$\mathbf{G}$的子群.
将$\mathbf{F}$分解成关于$\bar{G}^{\mathbf{k}_1}$的左陪集表示
\[\mathbf{F}=T_1\bar{G}^{\mathbf{k}_1}+T_2\bar{G}^{\mathbf{k}_1}+\cdots+T_q\bar{G}^{\mathbf{k}_1}\]这里$q=h/b$是在$\Gamma$中star的元素的数目,如果$T_i\mathbf{k}_i\equiv\mathbf{k}_i$,那么所有的左陪集元素$T_i\bar{G}^{\mathbf{k}_1}$就会将$\mathbf{k}_1$变换到$\mathbf{k}_i$,因此这里的左陪集和star的矢量$\mathbf{k}_1,\mathbf{k}_2,\cdots,\mathbf{k}_q$是一一对应的.
下面也可以根据$\mathbf{G}^{\mathbf{k}_1}$将空间群$\mathbf{G}$进行左陪集分解
\[\mathbf{G}=\{T_1\rvert\mathbf{x}_1\}\mathbf{G}^{\mathbf{k}_1}+\{T_2\rvert\mathbf{x}_2\}\mathbf{G}^{\mathbf{k}_1}+\cdots+\{T_q\rvert\mathbf{x}_q\}\mathbf{G}^{\mathbf{k}_1}\]并保持一一对应的关系,陪集${T_i\rvert\mathbf{x}_i}\mathbf{G}^{\mathbf{k}_1}$中的任何一个元素都可以将波矢为$\mathbf{k}_1$ 的Bloch函数变换到波矢为$\mathbf{k}_i$的Bloch函数.陪集${T_i\rvert\mathbf{x}_i}\mathbf{G}^{\mathbf{k}_1}$中的元素可以表示为${T_i\rvert\mathbf{x}_i}{S\rvert\mathbf{w}}$,这里${S\rvert\mathbf{w}}\in\mathbf{G}^{\mathbf{k}_1}$且满足
\[\{T_i\rvert\mathbf{x}_i\}\{S\rvert\mathbf{w}\}\psi_{\mathbf{k}_1}=\psi_{T_iS\mathbf{k}_1}(\mathbf{r-x}_i-T_i\mathbf{w})\]利用关系式$T_iS\mathbf{k}_1\equiv T_i\mathbf{k}_i\equiv\mathbf{k}_i$.小群$\mathbf{G}^{\mathbf{k}_1}$的性质是其中的操作元可以将波矢为$\mathbf{k}_1$的Bloch函数变成另外一个波矢为$\mathbf{k}_1$的Bloch函数.
在前面通过空间的表示$\Gamma$来去表示平移群$\mathbf{T}$从而得到了一系列的矢量$\mathbf{k}_1,\mathbf{k}_2,\cdots,\mathbf{k}_d$,而且利用空间群操作${S\rvert\mathbf{w}}$总可以由一个矢量$\mathbf{k}_i$标记的Bloch函数得到这个序列中其它的矢量$\mathbf{k}_j$标记的Bloch函数,这里可以提出一个问题,是否由$\Gamma$表示得到的这$d$个矢量都是不相同的,或者说$d=q$?
这里的$d$一定是$q$的整数倍$d=tq$,在$\mathbf{k}_1,\mathbf{k}_2,\cdots,\mathbf{k}_d$着个序列中,star $\mathbf{k}_1,\mathbf{k}_2,\cdots,\mathbf{k}_q$会重复出现$t$次.
下面来证明上面的结论
在空间群$\mathbf{G}$的元素中,要得到一个与$\psi_{\mathbf{k}_1}(\mathbf{r})$具有相同波矢$\mathbf{k}_1$的新Bloch函数,那么这个元素必定属于小群$\mathbf{G}^{\mathbf{k}_1}$,因为
\[\{S_i\rvert\mathbf{w}_i\}\in\mathbf{G}^{\mathbf{k}_1}\]所以
\[\{E\rvert\mathbf{t}\}\{S_i\rvert\mathbf{w}_i\}\]作用在
\[\psi_{\mathbf{k}_1}(\mathbf{r})\]上产生的都是波矢相同的Bloch函数,在基矢
\[\psi_{\mathbf{k}_1}(\mathbf{r}),\psi_{\mathbf{k}_1}(\mathbf{r}),\cdots,\psi_{\mathbf{k}_d}(\mathbf{r})\]中,波矢为$\mathbf{k}_1$的Bloch函数的可以组成线性无关的函数,假设它的数量为$b$,那么它们可以表示为
\[\{S_1\rvert\mathbf{w}_1\}\psi_{\mathbf{k}_1}(\mathbf{r}),\{S_2\rvert\mathbf{w}_2\}\psi_{\mathbf{k}_1}(\mathbf{r}),\cdots,\{S_b\rvert\mathbf{w}_b\}\psi_{\mathbf{k}_1}(\mathbf{r})\]假设找到了$t$个最大线性无关的函数
\[\psi_{\mathbf{k}_{1,1}},\psi_{\mathbf{k}_{1,2}},\cdots,\psi_{\mathbf{k}_{1,t}}\]从而可以得到
\[\sum_{i=1}^t\lambda_i\psi_{\mathbf{k}_{1,i}}=0\]因为这些函数是线性无关的,所以$\lambda_i=0(i=1,t)$;假设现在有
\[\sum_{i=1}^t\lambda_i\{T_j\rvert\mathbf{x}_j\}\psi_{\mathbf{k}_{1,i}}(\mathbf{r})=0\]在上式两端乘以
\[\{T_j\rvert\mathbf{x}_j\}^{-1}\]可以得到$\lambda_i=0,(i=1,t)$,因此函数
\[{T_j\rvert\mathbf{x}_j}\psi_{\mathbf{k}_{1,i}}(\mathbf{r})(i=1,t)\]是波矢为$\mathbf{k}_j$的线性无关的Bloch函数.
这里的$t$个波函数
\[\psi_{\mathbf{k}_{1,1}}(\mathbf{r}),\psi_{\mathbf{k}_{1,2}}(\mathbf{r}),\cdots,\psi_{\mathbf{k}_{1,t}}(\mathbf{r})\]构成了$\mathbf{k}_1$的小群$\mathbf{G}^{\mathbf{k}_1}$的不可约表示的基,它张开了一个不可约的子空间$V^{\mathbf{k}_1}$,通过这个基可以得到小群$\mathbf{G}^{\mathbf{k}_1}$的不可约表示,同样的也就可以得到空间群$\mathbf{G}$的不可约表示以及整个的线性空间$V$
\[V=\sum_j\{T_j\rvert\mathbf{x}_j\}V^{\mathbf{K}_1}\]如果$V^{\mathbf{K}_1}$是可约的
\[V^{\mathbf{K}_1}=U^{\mathbf{K}_1}\oplus W^{\mathbf{K}_1}\]那么$V$同样可以约化为
\[V=U\oplus W,\quad U=\sum_j\{T_j\rvert\mathbf{x}_j\}U^{\mathbf{K}_1},\quad W=\sum_j\{T_j\rvert\mathbf{x}_j\}W^{\mathbf{K}_1}\]空间群表示构建步骤
- (1):从布里渊区的表示域中选择一个波矢$\mathbf{k}_1$.
- (2):确定波矢$\mathbf{k}_1$的小共群$\bar{G}^{\mathbf{k}_1}$,其中的元素满足$S_j\mathbf{k}_1\equiv\mathbf{k}_1$,然后在空间群$\mathbf{G}$中构建$\mathbf{k}_1$的小群$\mathbf{G}^{\mathbf{k}_1}$.
- (3):确定包含波矢$\mathbf{k}_1$的star,或者是将空间群$\mathbf{G}$根据小群$\mathbf{G}^{\mathbf{k}_1}$进行左陪集分解,这些得到的左陪集和star中的矢量是一一对应的.
- (4):确定小群$\mathbf{G}^{\mathbf{k}_1}$的不可约表示$\Gamma_p^{\mathbf{k}_1}$,它的基矢具有额外的性质:它的元素是波矢为$\mathbf{k}_1$的Bloch函数,让这些组成函数序列 \(\psi_{\mathbf{k}_1,1}(\mathbf{r}),\psi_{\mathbf{k}_1,2}(\mathbf{r}),\cdots,\psi_{\mathbf{k}_1,t}(\mathbf{r})\) 这里的$\Gamma_p^{\mathbf{k}_1}$称为小群$\mathbf{k}_1$的小表示.
- (5):构建矢量空间$V$中的所有函数
这里的\({T_j\rvert\mathbf{x}_j}\)是空间群根据小群
\[\mathbf{G}^{\mathbf{k}_1}\]的左陪集表示,此时矢量空间$V$对于空间群$G$而言是不可约的,并且表示$\Gamma$的基函数有$d$个
\[{T_j\rvert\mathbf{x}_j}\psi_{\mathbf{k}_1,i}(\mathbf{r})\]函数,这里$dqt=ht/b$.
- (6):对所有的小表示$\Gamma_p^{\mathbf{k}_1}$重复上面的步骤,从而得到所有$\mathbf{k}_1$标记的star的空间群$\mathbf{G}$的表示.
- (7):对所有在表示区域(Representation domain)中的波矢$\mathbf{k}_1$进行上面的全部操作,最后就可以得到空间群$\mathbf{G}$的所有表示.
实际应用
在求解空间群不可约表示的时候,最重要的就是得到小群的不可约表示,但是此时又会发现小群本身又是一个空间群;在空间群$\mathbf{G}$的表示中,操作${E\rvert\mathbf{t}}$表示为对角矩阵,小群的元素${E\rvert\mathbf{t}}$对应的表示为一个标量矩阵$\exp(-i\mathbf{k}_1\cdot\mathbf{t})$的时候,情况就会变的不同,此时矩阵$\Gamma_p^{\mathbf{k}_1}$满足非常简单的规则.
先将小群$\mathbf{G}^{\mathbf{k}_1}$根据平移群$\mathbf{T}$进行陪集分解
\[\mathbf{G}^{\mathbf{k}_1}=\{S_1\rvert\mathbf{w}_1\}\mathbf{T}+\{S_2\rvert\mathbf{w}_2\}\mathbf{T}+\cdots+\{S_b\rvert\mathbf{w}_b\}\mathbf{T}\label{eq2}\]假设
\[\{S_i\rvert\mathbf{w}_i\}\{S_j\rvert\mathbf{w}_j\}=\{S_iS_j\rvert\mathbf{w}_i+S_I\mathbf{w}_j\}=\{E\rvert\mathbf{t}_{ij}\}\{S_k\rvert\mathbf{w}_k\}\]这里${E\rvert\mathbf{t}_{ij}}\in\mathbf{T}$,上式中有
\[\mathbf{t}_{ij}=\mathbf{w}_i+S_i\mathbf{w}_j-\mathbf{w}_k\]因为$\mathbf{t}_{ij}$是个平移则可以得到
\[\Gamma_p^{\mathbf{k}_1}(\{S_i\rvert\mathbf{w}_i\})\Gamma_p^{\mathbf{k}_1}(\{S_j\rvert\mathbf{w}_j\})=\exp(-i\mathbf{k}_1\cdot(\mathbf{w}_i+S_i\mathbf{w}_j-\mathbf{w}_k))\Gamma_p^{\mathbf{k}_1}(\{S_k\rvert\mathbf{w}_k\})\]从而对于小群中的元素${R\rvert\mathbf{v}}\in\mathbf{G}^{\mathbf{k}_1}$有
\[\Gamma_p^{\mathbf{k}_1}(\{R\rvert\mathbf{v}\})=\exp(-i\mathbf{k}\cdot\mathbf{v})\mathbf{D}_p^{\mathbf{k}_1}(\{R\rvert\mathbf{v}\})\label{eq1}\]从而可以得到
\[\mathbf{D}_p^{\mathbf{k}_1}(\{S_i\rvert\mathbf{w}_i\})\mathbf{D}_p^{\mathbf{k}_1}(\{S_j\rvert\mathbf{w}_j\})=\exp(-\mathbf{g}_i\cdot\mathbf{w}_j)\mathbf{D}_p^{\mathbf{k}_1}(\{S_k\rvert\mathbf{w}_k\})\label{eq3}\]这里$\mathbf{g}_i$是倒空间中的格矢,且$S^{-1}\mathbf{k}_1\equiv\mathbf{k}_1$,和$\mathbf{g}_i$相关联的方程为
\[S_i^{-1}\mathbf{k}_1\equiv\mathbf{k}_1+\mathbf{g}_i\]同样的,如果${E\rvert\mathbf{t}}\in\mathbf{T}$,那么从(\ref{eq1})中可以得到
\[\begin{equation}\begin{aligned}&\mathbf{D}_p^{\mathbf{k}_1}(\{E\rvert\mathbf{t}\})=\mathbf{1}\\ &\exp(-i\mathbf{g}_i\cdot(\mathbf{w}_j+\mathbf{t}))=\exp(-i\mathbf{g}_i\cdot\mathbf{w}_j)\end{aligned}\end{equation}\]从前面可以看到,对平移群的元素,$\mathbf{D}_p^{\mathbf{k}_1}$都是$\mathbf{1}$,因此对于陪集分解(\ref{eq2})来说,$\mathbf{D}_p^{\mathbf{k}_1}$对一个特定的陪集表示中的所有元素的矩阵表示都是相同的,也就是说$\mathbf{D}_p^{\mathbf{k}_1}$是关于陪集 $\mathbf{G}^{\mathbf{k}_1}/\mathbf{T}$的一个函数表示.
但是这个商群和$\bar{G}^{\mathbf{k}_1}$是同构的,从而可以说$\mathbf{D}_p^{\mathbf{k}_1}$是关于小共群元素的函数.因此将一个本来计算小群的表示问题转换成了研究对应的小共群的表示问题
将(\ref{eq3})改写为
\[\mathbf{D}_p^{\mathbf{k}_1}(S_i)\mathbf{D}_p^{\mathbf{k}_1}(S_j)=\exp(-i\mathbf{g}_i\cdot\mathbf{w}_j)\mathbf{D}_p^{\mathbf{k}_1}(S_k)\]这里$S_iS_j=S_k,S_i^{-1}\mathbf{k}_1=\mathbf{k}_1+\mathbf{g}_i$.
可以看到$\mathbf{D}_p^{\mathbf{k}_1}$是小共群$\bar{G}^{\mathbf{k}_1}$到一系列矩阵的同态,这里存在两个重要的情况:
-
(1):对所有的$j=1,b$都有$\mathbf{w}_j=0$,这对应着空间群$\mathbf{G}$是点式空间群的情况.
-
(2):对所有的$i=1,b$满足$S_i^{-1}\mathbf{k}_1=\mathbf{k}_1$,在这种情况下$\mathbf{k}_1$是布里渊区内部的一个点,因为此时和它等价的就只有它自身.
当$\mathbf{D}_p^{\mathbf{k}_1}$是同态时,它也是小共群的一个表示,而且$\Gamma_p^{\mathbf{k}_1}$的不可约性也意味着$\mathbf{D}_p^{\mathbf{k}_1}$是不可约的.因此对于上面的量中情况,所需要的做的就是找出小共群的不可表示,一旦它确定了之后,就可以通过(\ref{eq1})来得到$\Gamma_p^{\mathbf{k}_1}$的矩阵形式.
这里剩下的就是讨论当$\mathbf{k}_1$在布里渊区表面上与非点式空间群的情况.
如果$\mathbf{k}_1$是个一般的点,那么其小共群中的元素就只有恒等操作,这就回到了前面的情况(2),所以剩下要处理的就是非点式空间群中$\mathbf{k}_1$是个对称点或者它在对称线(面)上的情况.为了处理这类问题,需要先引入投影表示(projective representation).
投影表示:包含群元$H_i,i=1,\rvert\mathbf{H}\rvert$的群$\mathbf{H}$对应的一个非奇异的矩阵函数$\Delta$是$\mathbf{H}$的投影表示需要满足下面的规则: 对每个群元乘积$H_iH_j=H_k$这里总存在一个标量函数$\mu(H_i,H_j)$在这一对有序的$H_i,H_j$上满足
\[\Delta(H_i)\Delta(H_j)=\mu(H_i,H_j)\Delta(H_k)\label{eq4}\]对所有的$i,j,l$都有
\[\mu(H_i,H_jH_l)\mu(H_j,H_l)=\mu(H_iH_j,H_l)\mu(H_i,H_j)\]函数$\mu(H_i,H_j)$形成了投影表示$\Delta$所谓的因子系统(factor system).当$\mu(H_i,H_j)=1$对所有的$i,j$都满足时,投影表示就变成了原来的表示(就是前面的不可约表示),如果$\rvert\mu(H_i,H_j)\rvert=1$那么总是可能通过对$\Delta$进行一个等价变换使它是幺正的.到这里就得到了不可约投影表示的概念,当不可约幺正投影表示具有相同的因子系统时,可以得到
\[\sum_{j=1}^{\rvert\mathbf{H}\rvert}\Delta^i(H_j)_{pv}^{*}\Delta^k(H_j)_{qw}=\frac{\rvert\mathbf{H}\rvert}{d_i}\delta^{ik}\delta_{pq}\delta_{vw}\]对特征标则有
\[\sum_{j=1}^{\rvert\mathbf{H}\rvert}\xi^{i*}(H_j)\xi^k(H_j)=\rvert\mathbf{H}\rvert\delta^{ik}\]给定一个因子系统为$\mu$的投影表示,如果取
\[\Delta^{'}(H_i)=C_i\Delta(H_i)\quad\text{for all }i,\quad C_i\in\mathcal{C}\]对于方程(\ref{eq4})有
\[\Delta^{'}(H_i)\Delta^{'}(H_j)=\frac{C_iC_j}{C_k}\mu(H_i,H_j)\Delta^{'}(H_k)\]改写
\[\nu(H_i,H_j)=\frac{C_iC_j}{C_k}\mu(H_i,H_j)\label{eq5}\]就可以发现此时$\nu(H_i,H_j)$是投影表示$\Delta^{‘}$的因子系统.两个投影表示的因子系统如果满足(\ref{eq5})那么就说它们属于相同的类.因为他们之间的联系关系非常简单,所以在研究的时候只需要研究单独的一个因子系统就可以.
对一个给定的因子系统为$\mu$投影表示$\Delta$满足$\Delta(E)\Delta(E)=\mu(E,E)\Delta(E)$,从而有
\[\Delta(E)=\mu(E,E)\mathbf{1}\]如果对所有的$i$取$\Delta^{‘}(H_i)=\Delta(H_i)/\mu(E,E)$,则
\[\Delta^{'}(E)=\mathbf{1}\]根据(\ref{eq5})的$1/C_i=\mu(E,E)$对所有的$i$定义一个新的因子系统$\nu$,因为
\[\Delta^{'}(H_i)\Delta^{'}(E)=\nu(H_i,E)\Delta^{'}(H_i)\]因此一定有
\[\nu(H_i,E)=q\quad\text{for all }H_i\]同样的
\[\nu(E,H_i)=q\quad\text{for all }H_i\]一个有限群$\mathbf{H}$的因子系统的类的数目$m$是有限的,这些类可以和一个阶数为$m$的阿贝尔群的元素意义对应,称为$\mathbf{H}$的乘子(multiplier).
这个一一对应的关系表述为,将$\mathbf{M}$中的元素标记为$M_1,M_2,\cdot,M_m$,如果$\mu_p,\mu_q$是与$M_p,M_q$对应的类中的任任意一个因子系统,那么因子系统$\mu_r$对所有的$i,j$满足
\[\mu_r(H_i,H_j)=\mu_p(H_i,H_j)\mu_q(H_i,H_j)\label{eq6}\]它总是数目对应$M_r$的类中,这里$M_r=M_pM_q$.而且$\mathbf{M}$中每个元素的阶对应着$\mathbf{H}$中因子的阶.如果$M_p$的阶数为$\alpha_p$那么表示因子系统可以选择为对应$M_p$的类,它的值是所有1的$\alpha_p$的根的解.因此每个投影表示都等价于同一个类中的因子系统中的幺正矩阵1.$\mathbf{M}$中的单位元素$M_1$对应着一个类,它所有值都是1的因子系统.
对一个阶数为$\rvert\mathbf{H}\rvert$的有限群$\mathbf{H}$,它的乘子$\mathbf{M}$的阶数为$m$,可以构建一个阶数为$\rvert\mathbf{H}\rvert m$的群,此时$\mathbf{M}$与$\mathbf{H}_\mathbf{M}$中心的子群是同构的.
一个群的中心是由那些和群中所有元素都对应的元素构成的一个子群,这些元祖可以自成一类.
通过识别$\mathbf{M}$与它在\(\mathbf{H}_\mathbf{M}\)中的镜像,可以得到\(\mathbf{H}_\mathbf{M}/\mathbf{M}\)与$\mathbf{H}$是同构的.\(\mathbf{H}_\mathbf{M}\)被称为是$\mathbf{H}$的核(Kernel)为$\mathbf{M}$的中心拓展(Central extension).
假设现在有一个群$\mathbf{H}$,来构建它授予因子系统$\mu$的幺正不可约投影表示,先选择一个$\mu$对所有的$j,k$满足
\[\mu(H_j,H_k)=\exp(2\pi ia(H_j,H_k)/g)\]这里通过对$\mu(H_j,H_K)$可以知道$a(H_j,H_k),g$都是整数,而且满足$0\le a(H_j,H_k)<g-1$,并且有
\[a(H_j,E)=a(E,H_j)=0\label{eq7}\]由于$\mu(H_j,H_j^{-1})=\mu(H_j^{-1},H_j)$从而有
\[a(H_j,H_j^{-1})=a(H_j^{-1},H_j)\]结合(\ref{eq6})可以得到
\[a(H_i,H_jH_l)+a(H_j,H_l)=a(H_iH_j,H_l)+a(H_i,H_j),\text{ mod } g\]令$\mathbf{Z}_g$是个整数循环群包含$0,1,2,\cdots,(g-1)$.令$\mathbf{H}^{*}$包含$g\rvert\mathbf{H}\rvert$个元素$(H_j,\alpha)$一个来自于$\mathbf{H}$一个来源于$\mathbf{Z}_g$,通过下面的方程来定义乘法法则
\[(H_i,\alpha)(H_k,\beta)=(H_jH_k,\alpha+\beta+a(H_j,H_k))\label{eq7}\]此时的\(\mathbf{H}^{*}\)构成了一个群.这里的$g$个$(E,\alpha)$元素可以构成\(\mathbf{H}^{*}\)的一个子群,它与\(\mathbf{Z}_g\)是同构的,但是尽管\((H_i,0)\)与$\mathbf{H}$中的元素是一一对应的,它却并不构成一个群,因此\(\mathbf{H}^{*}\)并不是$\mathbf{H}$的子群.
从(\ref{eq6})和(\ref{eq7})可以得到对所有的$\alpha,\beta,k$都有
\[(E,\alpha)(H_k,\beta)=(H_k,\beta)(E,\alpha)=(H_k,\alpha+\beta)\]通过上式可以得到有$g$个元素$(E,\alpha)$的子群此时位于\(\mathbf{H}^{*}\)的中心,因为$(E,\alpha)$与它的所有元素都是对易的.根据 Schur’s引理如果$\Gamma$是\(\mathbf{H}^{*}\)的一个表示,那么$\mathbf{\Gamma}(E,\alpha)$就是一个标量乘以单位矩阵.
假设这里对$\mathbf{H}^{*}$存在一个表示,对所有的$\alpha\in\mathbf{Z}_g$都有
\[\mathbf{\Gamma}(E,\alpha)=\exp(2\pi i\alpha/g)\mathbf{1}\]那么
\[\mathbf{\Gamma}(H_k,\beta)=\mathbf{\Gamma}(H_k,0)\mathbf{\Gamma}(E,\beta)=\mathbf{\Gamma}(H_k,0)\exp(2\pi i\beta/g)\]改写$\mathbf{\Gamma}(H_k,0)=\Delta(H_k)$可以得到
\[\begin{equation}\begin{aligned}\Delta(H_j)\Delta(H_k)&=\mathbf{\Gamma}(H_k,\alpha)\mathbf{\Gamma}(H_k,\beta)\exp(-2\pi i(\alpha+\beta)/g)\\ &=\mathbf{\Gamma}(H_jH_k,\alpha+\beta+a(H_j,H_k))\exp(-2\pi i(\alpha+\beta)/g)\\ &=\Delta(H_jH_k)\exp(2\pi ia(H_j,H_k)/g)\end{aligned}\end{equation}\]从这里就可以看到$\Delta$是群$\mathbf{H}$的投影表示,因为$\Gamma$是幺正的,所以这个投影表示也是幺正的,它同时也是不可约的.
总之,如果$\Delta$是$\mathbf{H}$的一个幺正不可约投影表示,如果令
\[\mathbf{\Gamma}(H_k,\beta)=\Delta(H_k)\exp(2\pi i\beta/g),\text{for all }k,\beta\]那么$\Gamma$是$\mathbf{H}^{*}$的表示.
接下来回到小共群来看一下前面提及到的因子系统,将$\bar{G}^{\mathbf{k}_1}$替换$\mathbf{H}$,$D_p^{\mathbf{k}_1}$替换$\Delta$则有
\[\mu(S_i,S_j)=\exp(-i\mathbf{g}_i\cdot\mathbf{w}_j),\quad S_i^{-1}\mathbf{k}_1=\mathbf{k}_1+\mathbf{g}_i\]这里的$\mathbf{w}_i$是小群$\mathbf{G}^{\mathbf{k}_1}$在进行陪集分解时与$S_j$相关联的平移部分的矢量.从上式可以看出当$S_i=E$势$\mathbf{g}_i=0$,从而
\[\mu(E,S_j)=1,\quad\text{for all }j\]实例:cubic close-packed and diamond structures
下面通过两个例子来展示一下上面的理论知识,一个点式空间群$Fm3m(O^5_h)$是一个cubic close-packed和一个非点式空间群$Fd3m(O_h^7)$是一个diamond structures.
这两个空间群都是基于面心立方,F,布拉菲点阵信息可以从Table3.1中得到
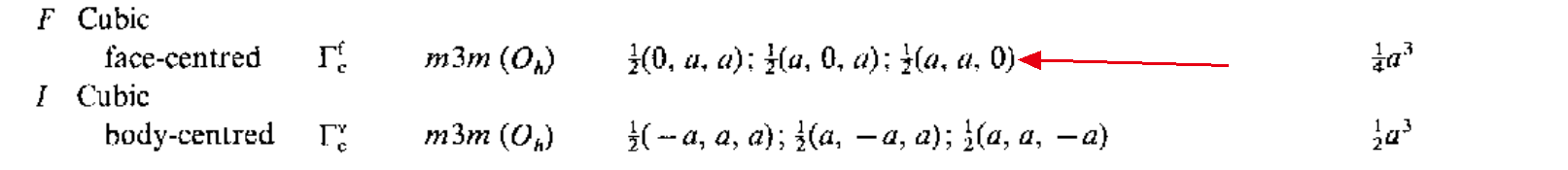
对应的点整平移基矢为
\[\left\{\begin{array}{c}\mathbf{t}_1=\frac{1}{2}(0,a,a)\\\mathbf{t}_2=\frac{1}{2}(a,0,a)\\\mathbf{t}_3=\frac{1}{2}(a,a,0) \end{array}\right.\]对于两种不同的晶体结构,它们的空间群的isogonal点群都是$m3m(O_h)$.
从Table3.3中可以得到倒空间中元胞的基矢为
\[\left\{\begin{array}{c}\mathbf{g}_1=\frac{2\pi}{a}(-1,1,1)\\ \mathbf{g}_2=\frac{2\pi}{a}(1,-1,1)\\ \mathbf{g}_3=\frac{2\pi}{a}(1,1,-1)\end{array}\right.\]
从Table3.7可以看到空间群$Fm3m(O_h^5)$的每个$m3m(O_h)$旋转操作都仅仅和一个纯的平移操作相联系,因此可以将空间群$Fm3m(O_h^5)$根据平移群$\mathbf{T}$进行陪集分解
\[Fm3m(O_h^5)=\sum_R\{R\rvert 000\}\mathbf{T}\]
这里的$R$是群$m3m(o_h)$中的所有元素.但是对于空间群$Fd3m(O_h^7)$只有属于子群$\bar{4}3m(T_d)$的操作才与纯平移操作相关联,它对应的配及分解为
\[Fd3m(O_h^7)=\sum_R\{R\rvert 000\}\mathbf{T}+\sum_R\{RI\rvert\frac{1}{4}\frac{1}{4}\frac{1}{4}\}\mathbf{T}\]这里$R$是属于$\bar{4}3m(T_d)$的元素,通常$I$表示反演操作.下面给出$\Gamma_c^f$的布里渊区中高对称点,线,面的信息
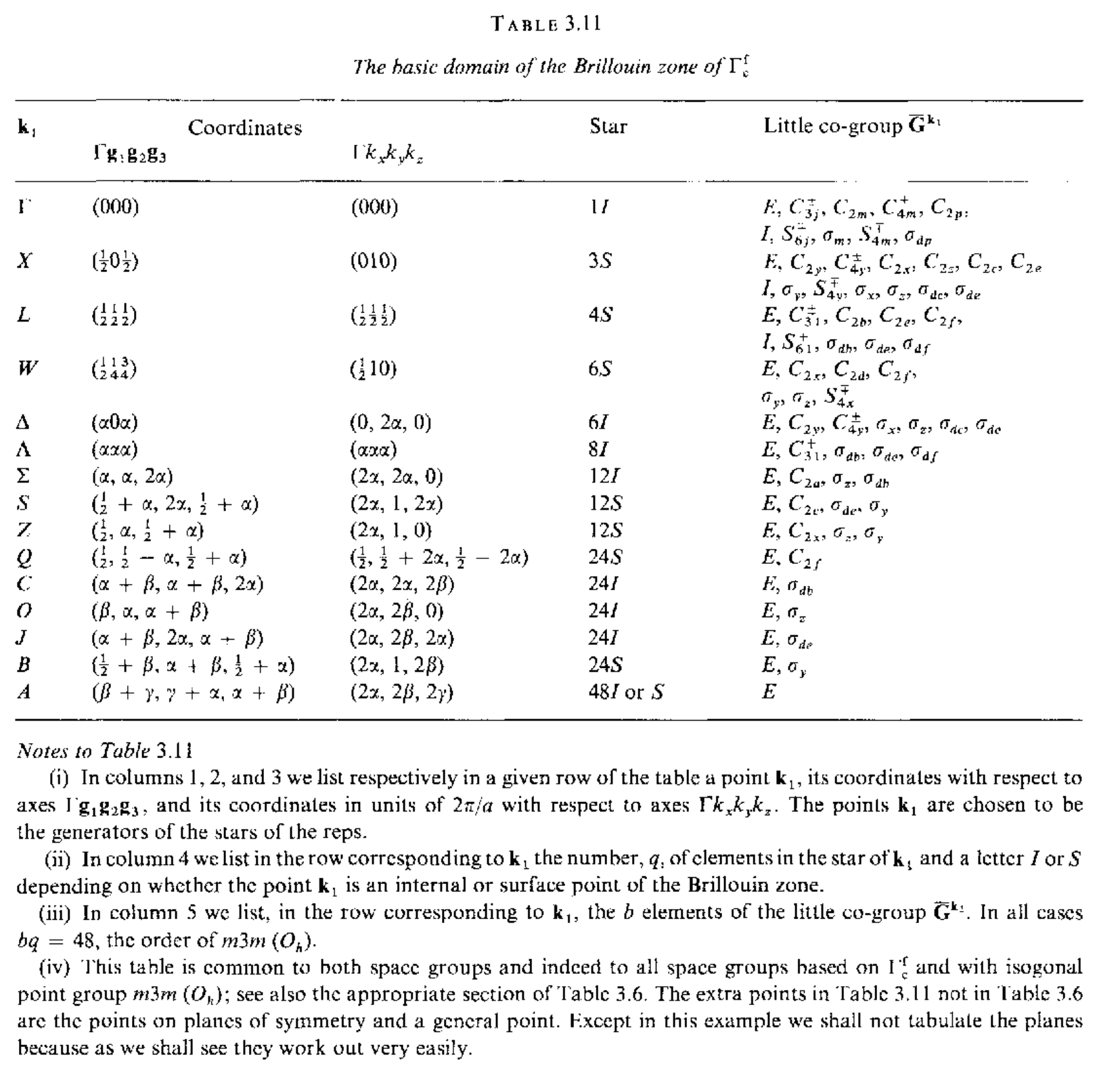
现在考虑将小群$\mathbf{G}^{\mathbf{k}_1}$根据平移群$\mathbf{T}$进行左陪集分解,对$Fm3m$有
\[\mathbf{G}^{\mathbf{k}_1}=\sum_S\{S\rvert 000\}\mathbf{T},\quad S\in\bar{G}^{\mathbf{k}_1}\label{eq8}\]对于$Fd3m$有
\[\mathbf{G}^{\mathbf{k}_1}=\sum_P\{P\rvert 000\}\mathbf{T}+\sum_Q\{Q\rvert\frac{1}{4}\frac{1}{4}\frac{1}{4}\}\mathbf{T}\]这里$P\in(\bar{\mathbf{G}}^{\mathbf{k}_1}\cap\bar{4}3m),Q$则是遍历$\bar{\mathbf{G}}^{\mathbf{k}_1}$中剩余的元素.
Fm3m
对于一个给定的$\mathbf{k}_1$需要决定$\bar{\mathbf{G}}^{\mathbf{k}_1}$的投影表示,它对应的因子系统为$\exp(-i\mathbf{g}\cdot\mathbf{w}_j)$,这里的$\mathbf{g}_i$是通过
\[S_i^{-1}\mathbf{k}_1=\mathbf{k}_1+\mathbf{g}_i\]来确定的,而$\mathbf{w}_j$则是由(\ref{eq8})的分解中与$S_j$相关联的平移部分来决定,很明显这里的$\mathbf{w}_j=0\quad\text{for all}\quad j$.因此因子系统就是一个单位矩阵,他属于小共群$\bar{\mathbf{G}}^{\mathbf{k}_1}$的乘子中与恒等元素相对应的类.从而 $\bar{\mathbf{G}}^{\mathbf{k}_1}$的合适的表示$D_p^{\mathbf{k}_1}$就正是原来的矢量表示,又因为$\bar{\mathbf{G}}^{\mathbf{k}_1}$是个点群,它的表示可以从Table2.2中得到.
小群
\[\mathbf{G}^{\mathbf{k}_1}\]的小表示
\[\Gamma_p^{\mathbf{k}_1}\]现在可以通过
\[\Gamma_p^{\mathbf{k}_1}(\{R\rvert\mathbf{v}\})=\exp(-i\mathbf{k}_1\cdot\mathbf{v})\mathbf{D}_p^{\mathbf{k}_1}(\{R\rvert\mathbf{v}\})\]立即得到,矩阵$\Gamma_p^{\mathbf{k}_1}$对应的可以得到
\[\mathbf{\Gamma}_p^{\mathbf{k}_1}(\{S\rvert\mathbf{t}\})=\exp(-i\mathbf{k}_1\cdot\mathbf{t})\mathbf{D}_p^{\mathbf{k}_1}(S)\]最终将空间群的表示求解回归到了矢量$\mathbf{k}_1$的小共群$\mathbf{G}^{\mathbf{k}_1}$表示的求解上.
Fd3m
这是一个非点式空间群,处理起来先要区分在陪集分解的时候
\[P\in{E,C_{3j}^\pm,C_{2m},\sigma_{dp},S_{4m}^\pm}\]的时候,平移部分$\mathbf{w}_i=0$,当
\[Q\in{I,S_{6j}^\mp,\sigma_m,C_{2p},C_{4m}^\pm}\]的时候平移部分
\[\mathbf{w}_j=\mathbf{v}=\frac{1}{4}(a,a,a)\]如果小群$\bar{G}^{\mathbf{k}_1}$只包含那些由$P$形成的元素,此时如果对所有的$i$都满足$\mathbf{g}_i=0$那么因子系统$\exp(-\mathbf{g}_i\cdot\mathbf{w}_i)$就是单位1,此时的$\mathbf{k}_1$来自于布里渊区中的内点${\Gamma,\Delta,\Lambda,\Sigma,C,O,J,A(I)}$.对于$Q$的情况,此时$\bar{G}^{\mathbf{k}_1}$则是由$\bar{4}3m(T_d){\Lambda,C,J,A(S)}$组成的.
当$\mathbf{k}_1={\Gamma,\Delta,\Lambda,\Sigma,C,O,J,A}$的时候,这里需要做的就是从Table2.2中查到$\bar{G}^{\mathbf{k}_1}$的表示$D_p^{\mathbf{k}_1}$.
在上面空间群Fm3m的求解中已经涉及到这些了,但是此时有一些区别的就是,对于Fd3m的陪集分解中包含$P$和$Q$的部分有
\[\mathbf{\Gamma}_p^{\mathbf{k}_1}(\{P\rvert\mathbf{t}\})=\exp(-i\mathbf{k}_1\cdot\mathbf{t})\mathbf{D}_p^{\mathbf{k}_1}(P)\] \[\mathbf{\Gamma}_p^{\mathbf{k}_1}(\{Q\rvert\mathbf{t+v}\})=\exp(-i\mathbf{k}_1\cdot\mathbf{t+v})\mathbf{D}_p^{\mathbf{k}_1}(Q)\]到这里,在明确的$P$或者$Q$的表示之后,就可以得到对应的小群的表示$\mathbf{\Gamma}_p^{\mathbf{k}_1}$.
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |