Julia,Python,Fortran,Mathematica循环计算速度比较
在平时进行数值计算时,我经常会遇到的两种比较消耗时间计算,其一是对大型矩阵的对角化问题,这是在对哈密顿量厄密矩阵求解本征问题时经常遇到的;另外一个就是循环计算了,这个结构在动量空间计算体系格林函数等其它量时,也会经常遇到。在这里首先对比一下各编程语言对循环的计算速度,然后根据我的经验提供一些加速的方法。
SSH model的Winding Number计算
在这篇博客中通过简单的SSH模型,来计算一下Winding Number这一拓扑不变量。虽然这个模型很简单,但是最近在学习Non-Hermitian的文章中,很多都是以这个模型为基础,研究非厄米体系的一些基本性质,其中也有通过计算非厄米系统的Winding Number来联系体系的拓扑性质。这里我就暂时不涉及非厄米的内容,因为我也只是对这个课题了解一点点内容,这里主要计算厄密SSH模型的Winding Number。

通过Wannier Center计算体系$Z_2$拓扑不变量
在$Z_2$拓扑不变量计算中,是通过一个比较直接的数值计算方法来对系统的$Z_2$拓扑不变量进行计算,而在学习能带拓扑的时候,最基本的理解都是通过电荷极化以及Wannier函数进行的,所以这里再利用Wannier Center的方法来计算体系的$Z_2$拓扑不变量,通过这个方法计算的时候,可以建立一个很清晰的物理图像,从而可以进一步加深对凝聚态物理中的拓扑有更深的理解。
$Z_2$拓扑不变量计算
前面学习了chern数的计算,其中其实遇到了波函数规范选择的问题,这个在计算时间反演不变系统的$Z_2$拓扑不变量的时候也会遇到,暂时我对这个规范问题也没有很好的理解,正好也通过计算$Z_2$拓扑不变量来对规范问题进行更进一步的了解,这里只是单纯的学习如何计算$Z_2$。
电子掺杂,空穴掺杂与化学势的关系
在研究超导问题的时候,不可避免的总会遇到体系时电子掺杂还是空穴掺杂,因为这两种不同的掺杂所对应的性质是不同的,最近重新温习一下超导的相关知识,正好也利用一个具体的紧束缚近似模型来说明一下电子和空穴掺杂到底是怎么回事,以及如何的通过自洽方法,通过调整化学势来决定体系到底是电子掺杂还是空穴掺杂
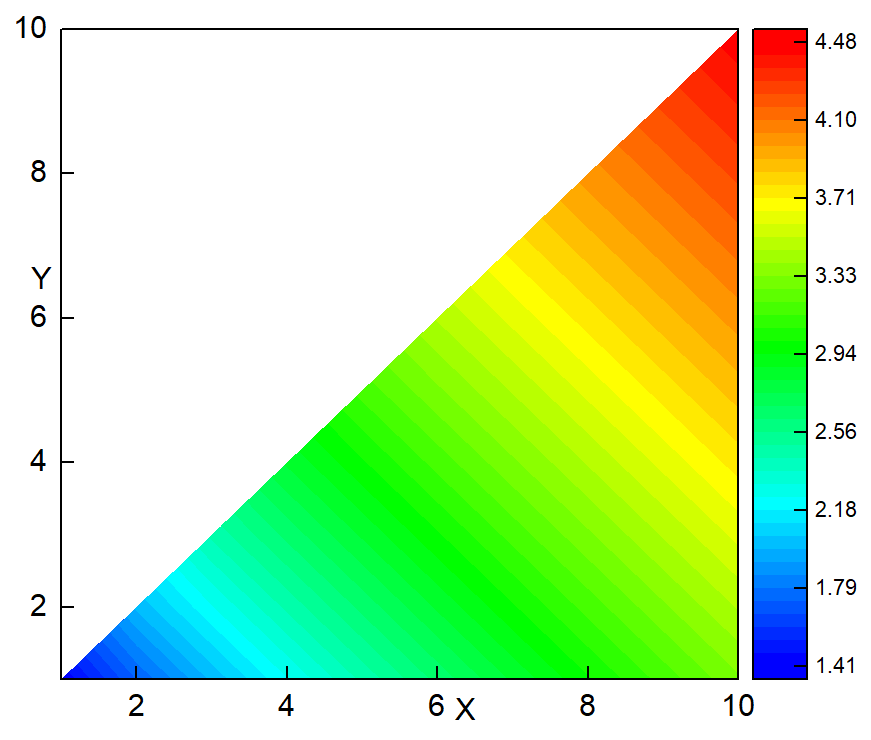
构建三角形或者平行四边形点阵
平时在做紧束缚模型的时候,都是在n*n的点阵上进行的,但是有时候可能也需要在三角形或者平行四边形样式的点阵上去计算一些性质,正好趁手头空闲就把这个做了一下,还是非常的简单。
Something just like this
虽然我并不是漫威动漫的忠实爱好者,但是这个系列确实很吸引人,正好最近学习到如何在博客中插入视频资源,来把博客内容变的更加丰富,就拿酷玩的这首歌配上蜘蛛侠来展示一下。
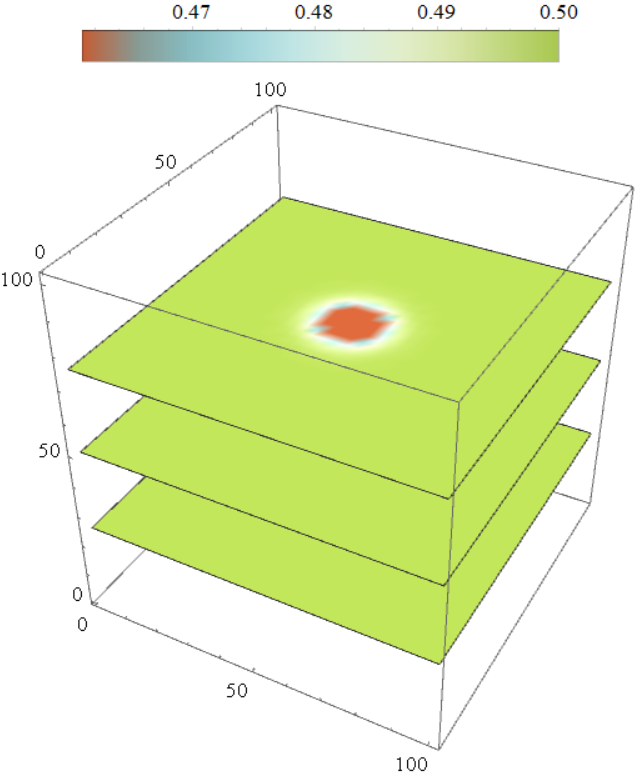
Mathematica高维度绘图及常用配色
在使用origin作图的过程中,发现其配色不是很丰富,而且一些高维图和向量图的做法并不是特别的友好,所以通过一番探索终于在Mathematica上实现了我自己平时科研中需要用到的一些作图,最主要的高维度作图展示,以及一些等能面的绘制。由于Mathematica同时也可以用来进行计算,而且对数据的操作也是非常方便,所以干脆将所有形式的图都利用Mathematica来绘制,后面有精力准备写一个自己的包,日常调用绘图即可,同时自动设置号图像大小、坐标轴样式以及图例等等。
共计 237 篇文章,24 页。
